What is a Parallelogram? Unveiling the Secrets of this Versatile Shape (2024)

Introduction

Have you ever wondered what makes certain shapes in geometry so special? Parallelograms are one of such fascinating shapes in geometry, known for their unique properties and versatile applications. From basic mathematics to advanced engineering, the concept of a parallelogram plays a crucial role in various fields. In this article, we will unravel the secrets of what is a parallelogram, explore its properties, and delve into the calculation of its area. Whether you’re a student looking to enhance your geometric knowledge or someone curious about the wonders of shapes, this article is for you.

What is a Parallelogram

Imagine a rectangle – that trusty shape you rely on for neat even cuts when wrapping a box. Now, take a moment to loosen its rigid structure. Let the opposite sides stretch a bit, but crucially, keep them perfectly parallel, like train tracks running side-by-side. This, my friends, is the essence of a parallelogram.

In simpler terms, what is a parallelogram? A parallelogram is a flat, four-sided figure (also known as a quadrilateral) where two sets of opposite sides run strictly parallel to each other. Think of it as a rectangle’s more relaxed cousin, where the focus is on parallel lines, not necessarily on right angles.

To solidify this concept, feast your eyes on the image below:

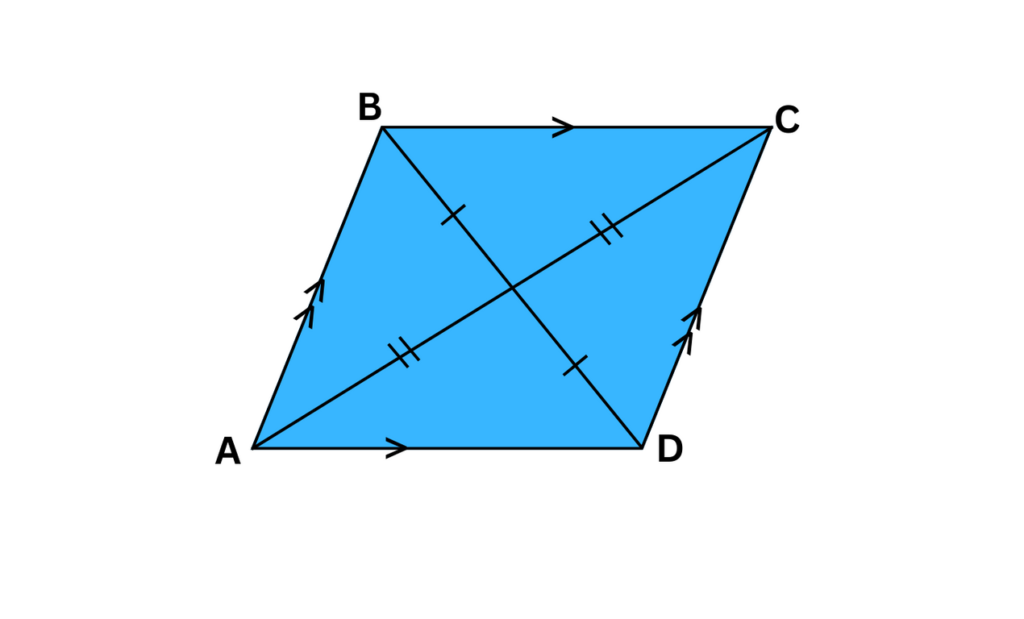
As you can see, this parallelogram has four sides, with opposite sides (AB and CD, as well as AD and BC) highlighted to emphasize their parallelism. This parallel magic is the foundation of a parallelogram’s identity.

Properties of a Parallelogram

Now that we’ve grasped the basic idea of what is a parallelogram, let’s delve deeper and explore its defining characteristics. These properties are like the building blocks that define the unique world of parallelograms:

• Opposite Sides: Remember those parallel lines we discussed earlier? Well, they bring another interesting property to the table. In a parallelogram, opposite sides (think of the sides where two parallel lines meet) are always congruent, meaning they have exactly the same length. So, if you measure the length of side AB, you can be confident that side CD will be exactly the same length.
• Opposite Angles: Here’s another treat brought to you by parallel sides. In a parallelogram, opposite angles (think of the angles where two sides meet at the corners that are not opposite each other) are always congruent as well. So, if you measure angle A and find it to be 60 degrees, its opposite counterpart, angle C, will also be a happy little 60-degree angle.
• Consecutive Interior Angles: This one might sound a bit more technical, but it’s actually quite intuitive. Imagine standing inside a parallelogram and looking at two angles that share a side but are not opposite each other (like angles A and B in the image). In the world of parallelograms, these consecutive interior angles are always supplementary, meaning they add up to exactly 180 degrees.
• Diagonals: Imagine drawing a line from one corner of the parallelogram to the opposite corner. These lines, which intersect (cross each other) inside the shape, are called diagonals. Here’s a cool twist: in a parallelogram, these diagonals bisect each other, meaning they cut each other in half at a point exactly in the middle.

Types of Parallelogram

The world of parallelograms isn’t confined to just one kind. Just like snowflakes, these shapes can exhibit some fascinating variations:

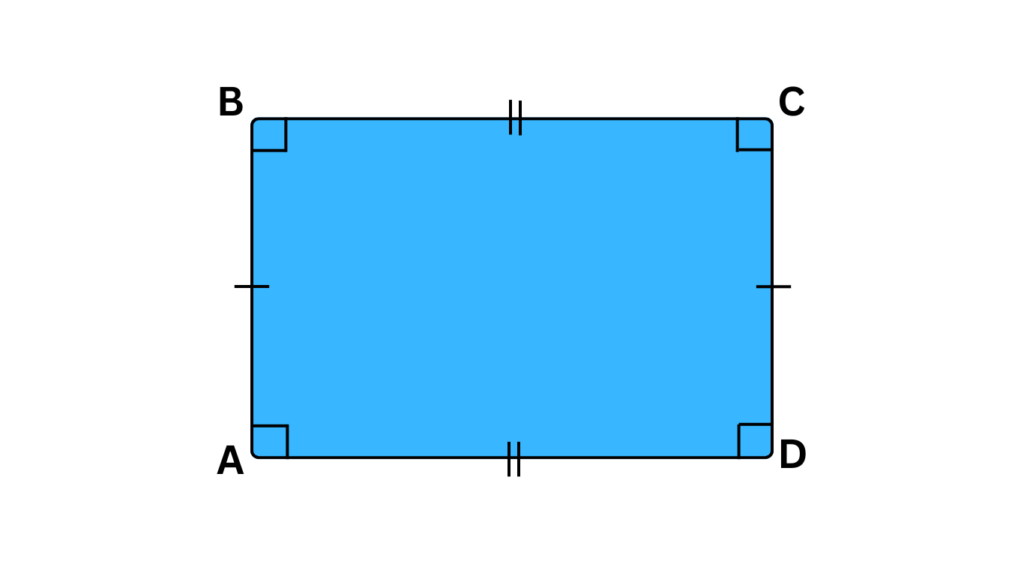
• The Classic Rectangle: Ever wonder if your trusty rectangular friend secretly belongs to another club? Well, surprise! A rectangle can be considered a special type of parallelogram. Why? A rectangle fulfills all the defining characteristics of a parallelogram – opposite sides parallel and equal in length, opposite angles congruent, and consecutive interior angles supplementary. However, a rectangle goes a step further by having all four angles measure exactly 90 degrees (right angles). So, while all rectangles are parallelograms, not all parallelograms are rectangles.

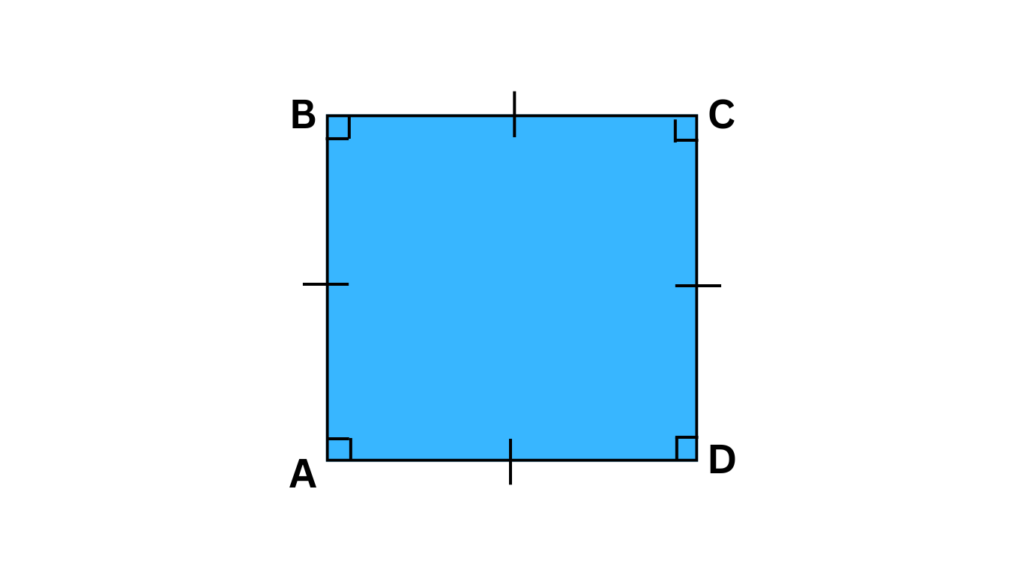
• The Square: This one might seem like a no-brainer after learning about rectangles. A square, with its four equal sides and four right angles, is also a special type of parallelogram. It fulfills all the requirements of a rectangle (and hence, a parallelogram) but takes it a step further by having all four sides equal in length.

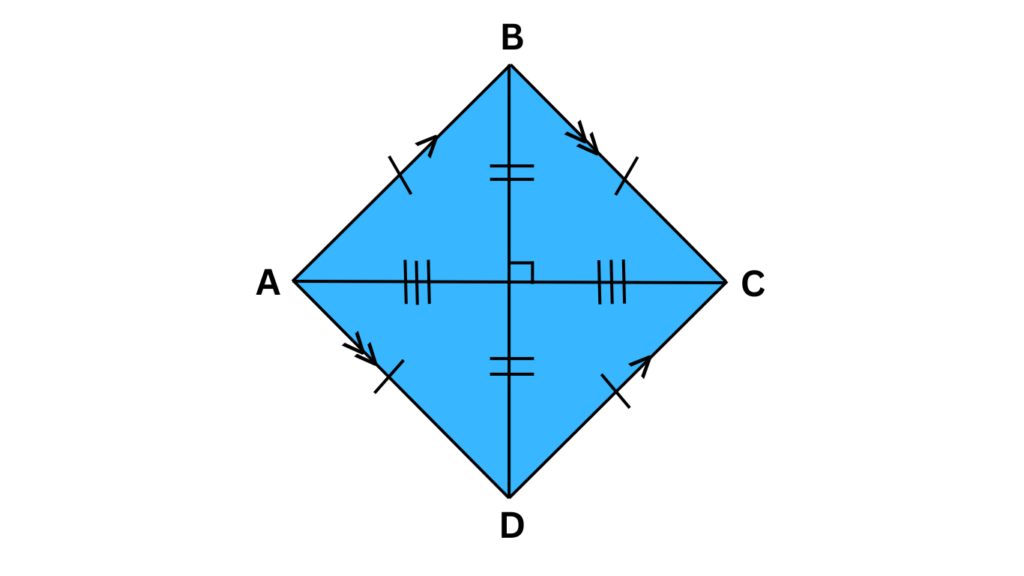
• The Rhombus: Ah, the rhombus – a shape that adds a touch of elegance to the parallelogram family. A rhombus shares some properties with a parallelogram, like having opposite sides parallel and equal in length. However, unlike a regular parallelogram, a rhombus doesn’t have to have perpendicular sides (meaning its angles might not be right angles). However, it does have a unique property: its diagonals bisect each other at a 90-degree angle (creating a perfect right angle where they intersect). So, imagine a parallelogram where all four sides are equal, but the angles aren’t necessarily right angles – that’s the essence of a rhombus.

Calculating the Area and Perimeter of a Parallelogram

Area

The area of a parallelogram can be calculated using the formula:

Area of a Parallelogram = Base x Height

Where the base is the length of one of the parallel sides, and the height is the perpendicular distance between the base and its opposite side. This formula is derived from the fact that a parallelogram can be transformed into a rectangle without changing its area by rearranging parts of it.

Example:

Let’s consider a parallelogram with a base of 6 units and a height of 4 units. Using the formula, we can calculate the area as:

Area = 6 x 4 = 24 square units

Perimeter

The perimeter of a parallelogram is the sum of the lengths of all its sides, which can be calculated as:

Perimeter of a Parallelogram = 2 x (Base + Side Length)

Example:

For a parallelogram with a base of 8 cm and a side length of 6 cm:

Perimeter = 2 x (8 cm + 6 cm) = 28 cm

Real-Life Applications of Parallelograms

The beauty of geometry lies in its ability to weave its magic into the fabric of our everyday lives. And the parallelogram shape is no exception. We just do not learn what is a parallelogram and how to find its area only for the sake of learning. Here are some surprising places where you might encounter parallelograms:

• Floor Tiles: Take a moment to appreciate the floor beneath your feet. Many floor tiles are designed as parallelograms, creating a neat, organized pattern that adds a sense of balance and structure to a room.
• Tabletops: Ever wondered why most tabletops are rectangular? It’s all thanks to the stability and balance that the parallelogram shape provides. With its opposite sides parallel and equal in length, a rectangular tabletop ensures a level surface for all your activities.
• Roof Trusses: Look up at the ceiling of any building with a pitched roof. Those intricate structures supporting the roof are often designed using trusses – assemblies of connected elements that create a strong and stable framework. And guess what shape many of these trusses are built upon? You guessed it – parallelograms. Their inherent strength and ability to distribute weight evenly make them ideal for supporting roofs.

How to Identify a Parallelogram

Now that we have learned all the things about parallelogram, i.e. from what is a parallelogram to calculating the area and perimeter of a parallelogram, you must be feeling like a parallelogram pro. As a pro, do you want to impress your friends with your newfound ability to spot these shapes in the wild? Here’s a simple guide to help you identify parallelograms with ease:

1. Look for Parallel Lines: The first and foremost sign of a parallelogram is the presence of two sets of parallel lines. Scan the shape and see if opposite sides run perfectly parallel to each other.
2. Check Opposite Sides: Once you’ve identified parallel lines, take a closer look at the opposite sides. In a true parallelogram, these opposite sides will always be the same length. Grab a ruler if needed to confirm.

Conclusion

Therefore, parallelograms are more than just simple geometric shapes; they hold significant importance in both mathematics and the real world. From their unique properties to their practical applications in various fields, understanding what is a parallelogram enriches our appreciation of geometry. Whether you encounter them in architecture, engineering, or everyday objects, the parallelogram’s fascinating characteristics make it a shape worth knowing. So next time you see a four-sided figure, take a moment to consider if it might be a parallelogram and marvel at its geometric beauty.

Frequently Asked Questions (FAQs)

What is a parallelogram in simple terms?

A parallelogram is a four-sided shape where opposite sides are parallel and equal in length.

How is a parallelogram different from a rectangle?

A rectangle is a type of parallelogram with all angles equal to 90 degrees.

How do you find the area of a parallelogram?

The area is calculated using the formula: Base × Height.