If you are wondering why the fundamental concept of geometry – types of angles, even needs to be studied then just look at a slice of pizza – a perfect triangular point, or the architectural design of buildings that stand so tall and strong.
These geometric gems are everywhere you look, playing a crucial role in shaping our world and forming the building blocks for understanding shapes, figures, and spatial relationships. But with terms like “acute,” “obtuse,” and “reflex” angles swirling around, things can get a bit confusing. Fear not, geometry enthusiast, for this article is your one-stop guide to conquering the wonderful world of angles.
The Importance of Angles
First, let us start with why these angles are important to learn and whether are they even worth learning. Angles are more than just fancy mathematical terms. They hold immense importance in various fields, from the foundation of mathematics itself to the practicalities of everyday life. In geometry, angles form the cornerstones of shapes, influencing their properties like area, perimeter, and symmetry. Architects use angles to design buildings with stability and aesthetics, ensuring roofs don’t cave in and walls stand tall. Engineers rely on angles to create bridges that can withstand heavy loads and airplanes that fly smoothly through the air.
Even seemingly mundane tasks involve angles. Look at the hands on a clock – the angle between the hour and minute hand tells you the time. Notice the slope of a ramp for wheelchairs – the angle determines its ease of use. Angles are truly woven into the fabric of our world, waiting to be explored and understood.
What is an Angle?
An angle is a fundamental geometric concept that defines the rotation between two intersecting lines or rays. It consists of three key components: a vertex, which marks the point of intersection, and two arms that extend from the vertex. The degree measure of an angle quantifies the extent of rotation between its arms, ranging from 0° to 360°.
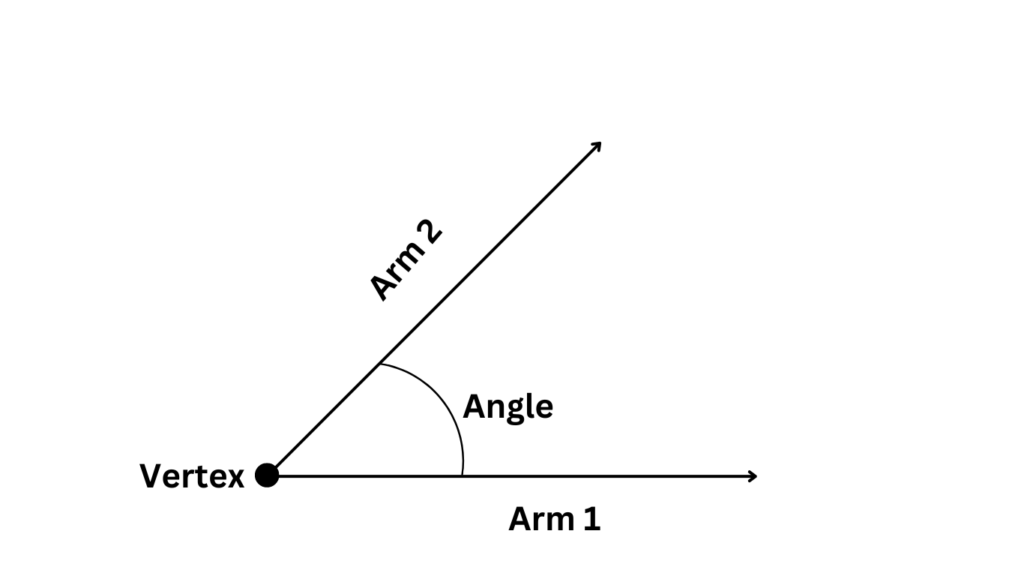
Types of Angles
Before diving into the fascinating world of different angles, let’s establish a common language for measurement. Angles are measured in degrees (°), denoted by a small circle placed after the number. Imagine a delicious pie – a full circle is divided into 360 equal slices, representing 360 degrees. Now, let’s explore the different types of angles, each with its unique properties and characteristics:
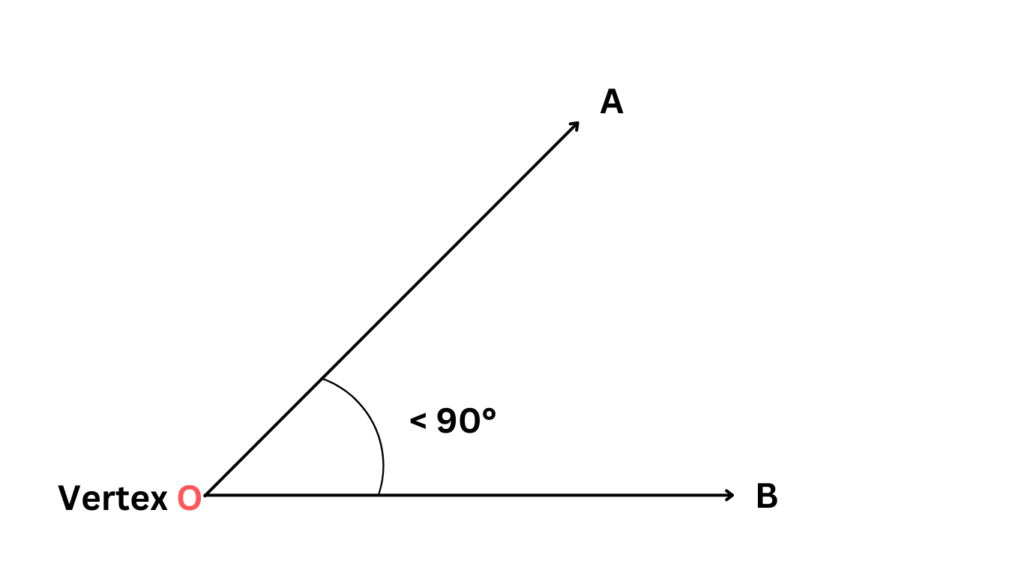
- Acute Angles:
Actue angles are those types of angles that measure less than 90 degrees. Picture a slice of pizza – the pointy corner where the crust meets the topping forms an acute angle. Acute angles are like sharpshooters, always precise and less than a right angle.
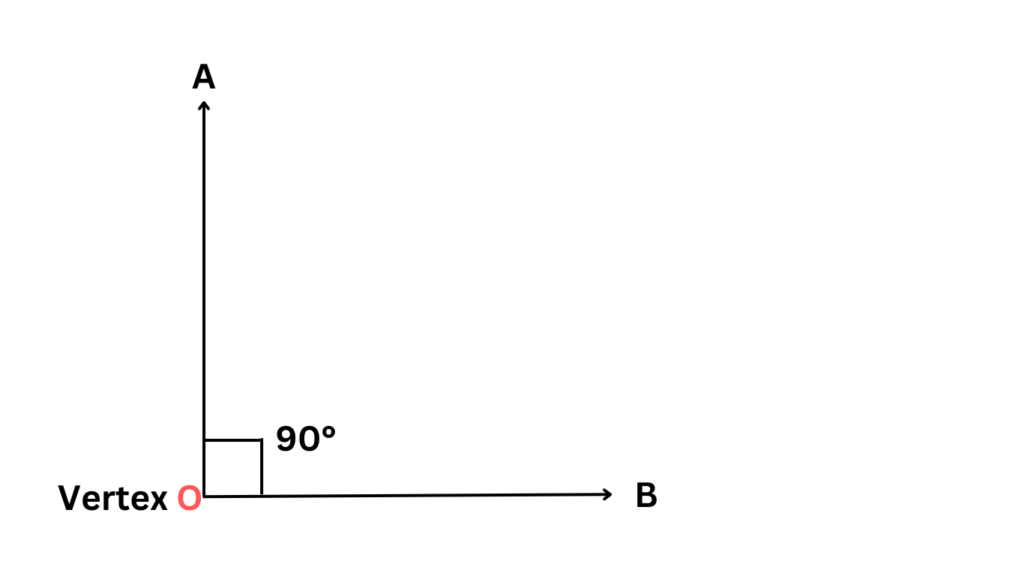
- Right Angles:
As the name suggests, right angles are those types of angles that measure exactly 90 degrees. Imagine a perfectly square book lying flat on a table. The corner where the cover meets the pages forms a right angle – a precise 90-degree bend, like a perfect salute.
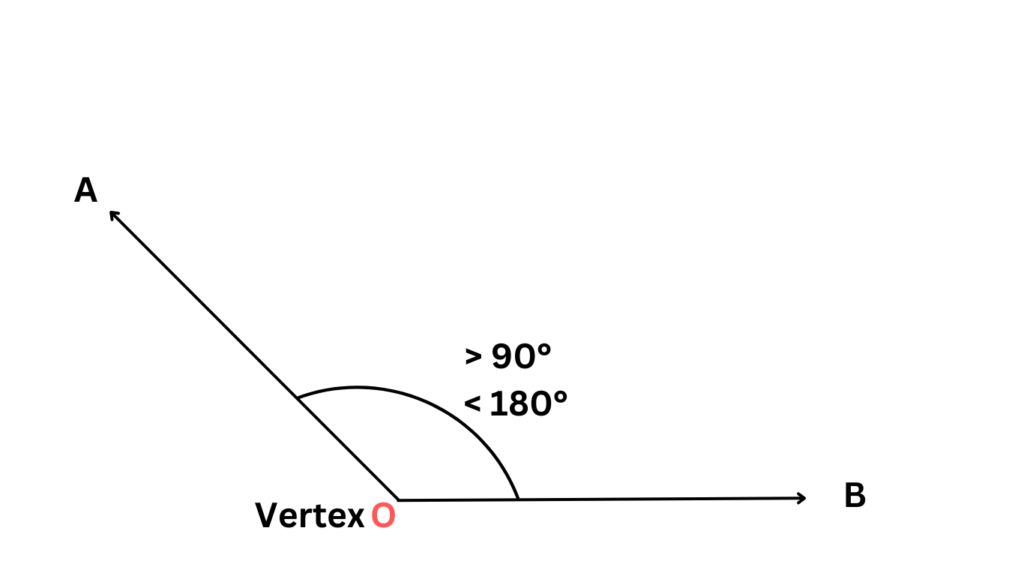
- Obtuse Angles:
Obtuse angles are those types of angles that measure between 90 degrees and 180 degrees. Think of the leaning Tower of Pisa – the angle formed by the tilted tower and the ground is obtuse, wider than a right angle but not quite a straight line.
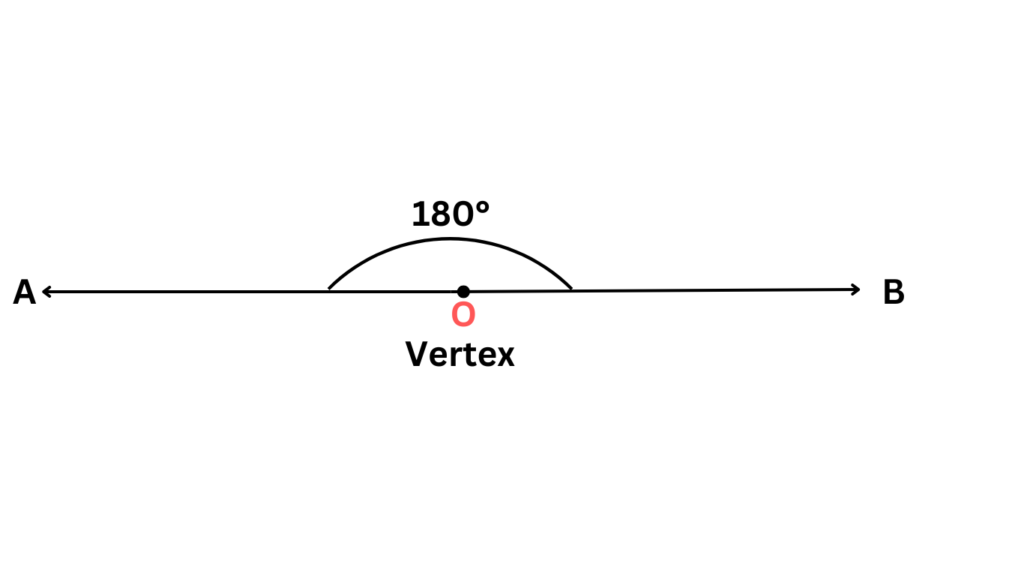
- Straight Angles:
Formed by two opposite rays extending in a straight line, straight angles measure exactly 180 degrees. Imagine opening a door all the way – the angle between the door and the wall when fully open is a straight angle, a complete 180-degree turn.
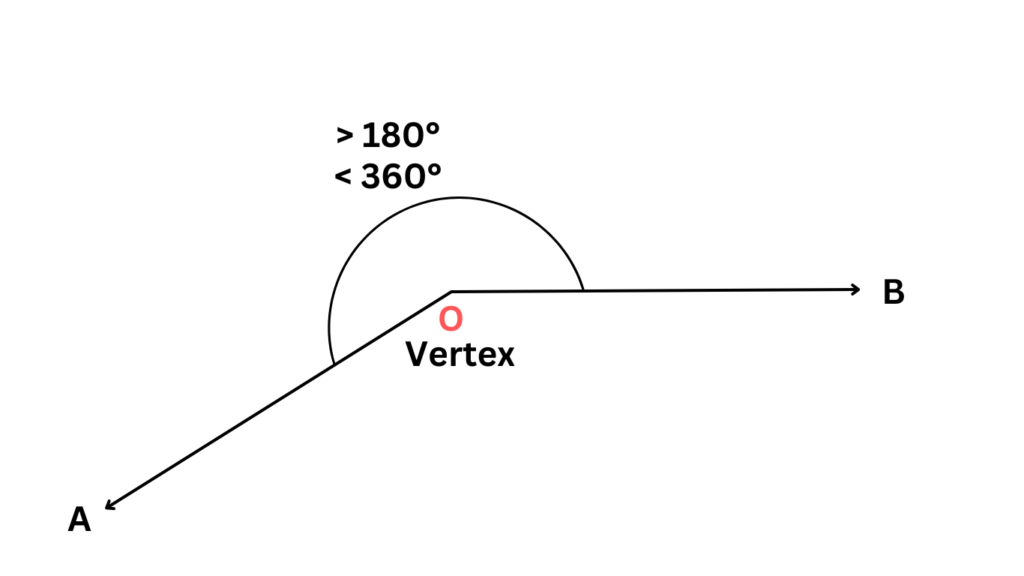
- Reflex Angles:
Reflex angles are those types of angles that measure between 180 degrees and 360 degrees. Imagine a U-turn on the road – the angle your car makes during the turn is a reflex angle, bending past a straight angle but not completing a full circle.
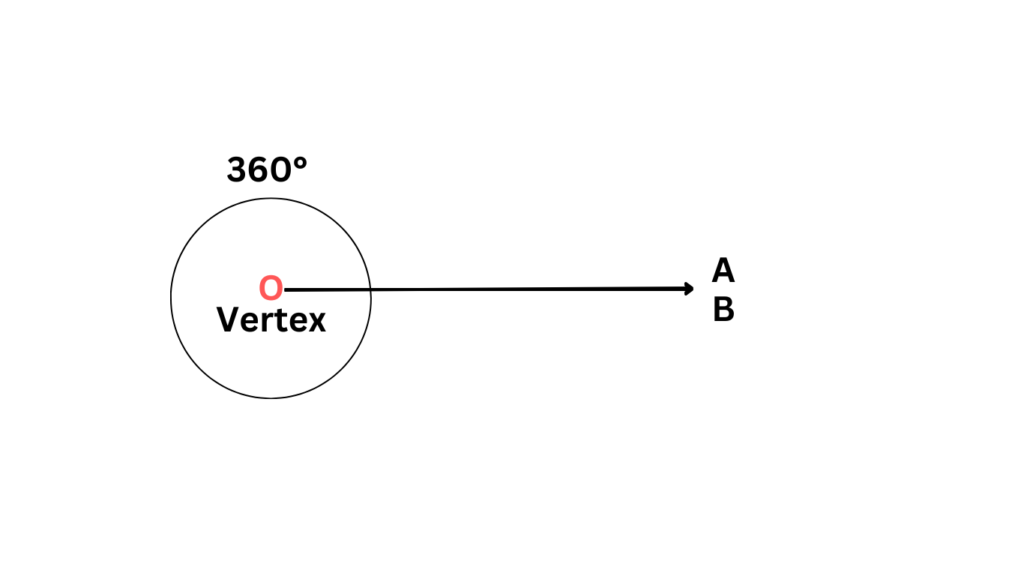
- Full or Complete Angles:
Finally, the final types of angles we have is a full angle also called a complete angle or a revolution, which measures a whopping 360 degrees. It represents a complete circle, like the hands of a clock completing a full rotation.
Mastering the Art of Drawing Angles
Now that you’re familiar with the different types of angles, let’s equip you with the tools to draw them yourself. Here’s what you’ll need:
- Ruler: A trusty ruler helps you draw straight lines, which form the arms of the angle.
- Protractor: This hero of the angling world is a semi-circular tool marked with degrees. It helps you measure and draw angles with precision.
- Pencil: To sketch your angles and make any necessary adjustments.
- A Compass (Optional): You can also draw the angles with a compass instead of a protractor, but this is for the advanced level.
Here are the steps to draw different types of angles using a protractor:
- Step 1: Mark the Vertex
This is the starting point, the point where the two rays of the angle meet. Make a small dot with your pencil to represent the vertex.
- Step 2: Drawing the Initial Arm
Using your ruler, draw a straight line extending outwards from the vertex. This is the first arm of your angle.
- Step 3: Measuring and Marking the Angle’s Degree
Here’s where the protractor comes in. Align the center of the protractor’s base (the straight edge without markings) exactly on the vertex point. Make sure one of the protractor’s arms coincides with the initial arm you drew in step 2.
- Step 4: Drawing the Second Arm
Now, locate the degree measurement on the protractor’s scale that corresponds to the desired angle type (acute, right, obtuse, etc.). For example, for an acute angle (less than 90°), locate a value between 0° and 90° on the scale. Place a small mark on the second arm of the protractor at that degree point.
- Step 5: Connecting the Dots
Finally, use your ruler to draw a straight line from the vertex point to the mark you made on the second arm of the protractor. This line represents the second arm of your angle, completing its formation.
Alternative Drawing Methods Using Compass
For those seeking an extra challenge, you can explore drawing angles using a ruler and compass – a more traditional, geometric approach. This method involves specific compass techniques to create precise angles based on their degree measurements. The initial steps are the same as using a protractor, you first mark a vertex then draw the first line.
After drawing the first line, you will take your compass and take measurements of the second line from the ruler and mark the point for the second. Finally, you connect the dots and draw the second line, and Walla!! you will get your desired types of angles. However, for beginners, mastering the protractor method is a solid foundation for drawing angles with confidence.
Measuring Angles
Now that you can draw angles, let’s delve into the world of measuring them! Here’s where the trusty protractor shines:
- Understanding the Protractor’s Scale: As mentioned earlier, the protractor is a semi-circular tool with markings along its curved edge. These markings represent degrees, typically ranging from 0° to 180°.
- Placing the Protractor Correctly on the Angle: Align the protractor’s center point (usually marked with a small notch) with the vertex of the angle you want to measure. Ensure one arm of the protractor coincides with one arm of the angle.
- Reading and Interpreting Angle Measurements: Follow the second arm of the angle until it intersects the protractor’s scale. The degree value at that point indicates the measure of the angle.
Angle Relationships
So far, we’ve explored the different types of angles and how to draw and measure them. But the world of angles goes beyond individual measurements. Angles can interact with each other in fascinating ways, forming specific relationships that govern the shapes they create. Let’s delve into some of these key angle relationships:
1. Vertical Angles:
Imagine standing at a crossroads. The two angles formed between the intersecting streets are called vertical angles. These special angles are always congruent (exactly equal in measure) because they are positioned directly opposite each other across a straight angle (180°). Think of it as a mirror image – the angles on either side of the straight line perfectly reflect each other.
2. Adjacent Angles:
Adjacent angles share a common vertex and one arm but have different second arms. Imagine a book lying open flat on a table. The two angles formed where the pages meet the cover are adjacent angles. They are not necessarily equal in measure, but when added together, they always equal 180 degrees.
3. Complementary and Supplementary Angles
- Complementary Angles: These charming duos add up to form a right angle (90°). Picture a delicious right triangle – the two non-right angles in the triangle are complementary angles. They work together to complete the 90-degree space of the right angle.
- Supplementary Angles: These helpful partners add up to form a straight angle (180°). Imagine a straight line being cut in half by a transversal line (a line intersecting two or more coplanar lines at distinct points). The two angles formed on one side of the transversal line (where the cut separates the line) are supplementary angles. They work together to fill the entire 180-degree space of a straight line.
Understanding these angle relationships is essential for solving various geometry problems and analyzing shapes. They form the building blocks for theorems and proofs, allowing you to predict and explain the properties of different figures.
Angles Beyond Textbooks: The Real-World Applications
The fascinating world of types of angles doesn’t stop at classroom exercises. They play a crucial role in various practical applications:
- Architecture and Engineering: From designing bridges that can withstand heavy loads to constructing structurally sound buildings, angles and types of angles are vital for ensuring stability and functionality. Architects and engineers use precise angles to calculate load distribution, optimize material usage, and create aesthetically pleasing structures.
- Navigation and Cartography: Angles are instrumental in navigation and mapmaking. Sailors and pilots use angles to determine their position and direction using tools like sextants and compasses. Cartographers rely on angles to create accurate maps, ensuring distances and directions are represented precisely.
- Interior Design and Art: Angles influence the visual appeal and functionality of interior spaces. Angles in furniture design determine comfort and ergonomics. Artists use angles to create depth, perspective, and balance in their compositions.
The applications of angles are truly vast, encompassing fields like physics (analyzing forces and motion), astronomy (calculating planetary positions), and even graphic design (creating layouts and user interfaces). As you explore different disciplines, you’ll discover even more ways angles shape our world and find different types of angles most of the shapes.
Conclusion
From the slice of pizza you enjoy to the skyscraper that graces your city skyline, angles are fundamental building blocks in our world. They play a vital role in geometry, forming the foundation for understanding shapes, figures, and spatial relationships. With the knowledge of different types of angles, their measurement techniques, and their fascinating relationships, you’re now equipped to explore the world with a newfound appreciation for these geometric gems.
So, the next time you encounter an angle, don’t be intimidated! Remember the tools and concepts you’ve learned in this article. Whether it’s drawing an angle, measuring its degree, or recognizing its relationship with other angles, you know how to conquer the wonderful world of angles.
Feeling inspired to explore further?
Here are some ideas:
- Try applying your newfound knowledge to solve real-world problems involving types of angles.
- Challenge yourself with more intricate angle relationships, like supplementary angles formed by multiple intersecting lines.
- Explore the various applications of angles in different fields like architecture, engineering, or animation.
Frequently Asked Questions (FAQs)
What are the different types of angles?
Angles can be classified into various types based on their degree measures and geometric properties. Common types include acute angles, right angles, obtuse angles, straight angles, reflex angles, and full angles.
How do I draw angles accurately?
To draw angles accurately, you’ll need essential tools such as a ruler, protractor, and pencil. Start by marking the vertex, then draw the initial arm and measure the angle’s degree before drawing the second arm. Practice exercises and explore alternative methods to enhance your drawing skills.
What are some practical applications of angles?
Angles find applications in diverse fields such as architecture, engineering, design, navigation, and geography. From designing buildings and structures to navigating through oceans and skies, angles play a pivotal role in shaping our world and understanding spatial relationships.