What is a Trapezoid? Unravel the Mystery of the 4-Sided Shape with a Twist

Introduction

Imagine you’re walking across a bridge, sitting at a trapezoidal table, or even admiring a famous piece of architecture. Trapezoids are all around us, subtly shaping the world in ways we often overlook. But what exactly is a trapezoid? Today, we’re diving deep into the world of trapezoids to uncover their secrets, understand their properties, and explore their significance in both everyday life and complex fields like engineering and architecture. So, let’s embark on this geometric journey and unlock the secrets of trapezoids!

What is a Trapezoid?

Imagine a four-sided shape, a quadrilateral, but with a twist – unlike a rectangle or a square with their neat, parallel sides all around, a trapezoid has only one pair of parallel sides. Think of a slice of birthday cake, a traffic sign, or even the roof of your house! These everyday objects all share the characteristic feature of a trapezoid – that unique, flat top and bottom.

Here’s a more formal definition what is a trapezoid? A trapezoid, also known as a trapezium in some parts of the world, is a four-sided polygon, or quadrilateral, with at least one pair of parallel sides. These parallel sides are referred to as the bases of the trapezoid, while the non-parallel sides are called the legs. This simple yet distinctive shape plays a crucial role in geometry and various practical applications. Now that we have understood what is a trapezoid, let us dive deep into some of its characteristics.

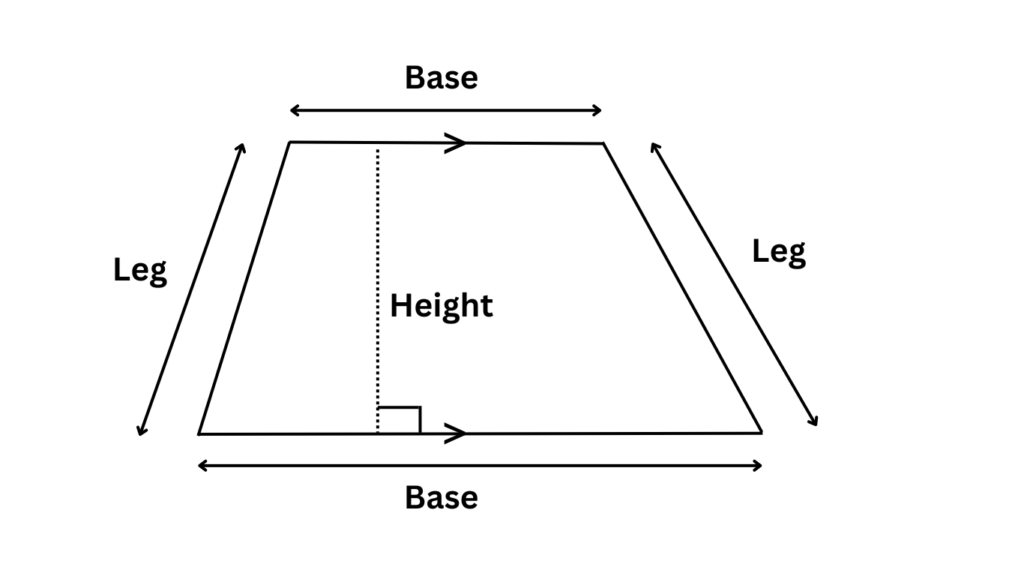
Characteristics of a Trapezoid

A trapezoid is defined by its unique properties:

• Bases: The two parallel sides of a trapezoid are called the bases. They can be of different lengths.
• Legs: The non-parallel sides are known as the legs. These can be equal in length, as in an isosceles trapezoid, or different, as in a scalene trapezoid.
• Height: The perpendicular distance between the bases is called the height or altitude.

Types of Trapezoids

Just like snowflakes (okay, maybe not that unique!), not all trapezoids are created equal. There are different “flavors” depending on the lengths of their sides and angles. Let’s explore the most common types:

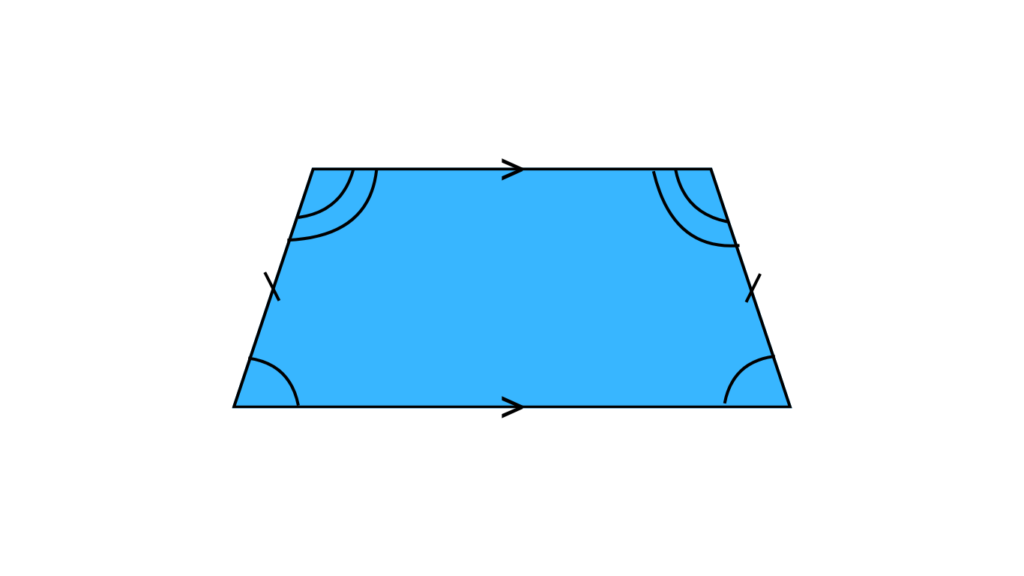
• Isosceles Trapezoid: This charming trapezoid has a special trick up its sleeve – its two legs are equal in length. Imagine a perfect slice of pizza, where the crust on both sides is exactly the same size. Additionally, the angles at the base (where the leg meets the base) are also congruent (meaning they have the same measure). So, next time you grab a slice, appreciate the mathematical beauty of an isosceles trapezoid.

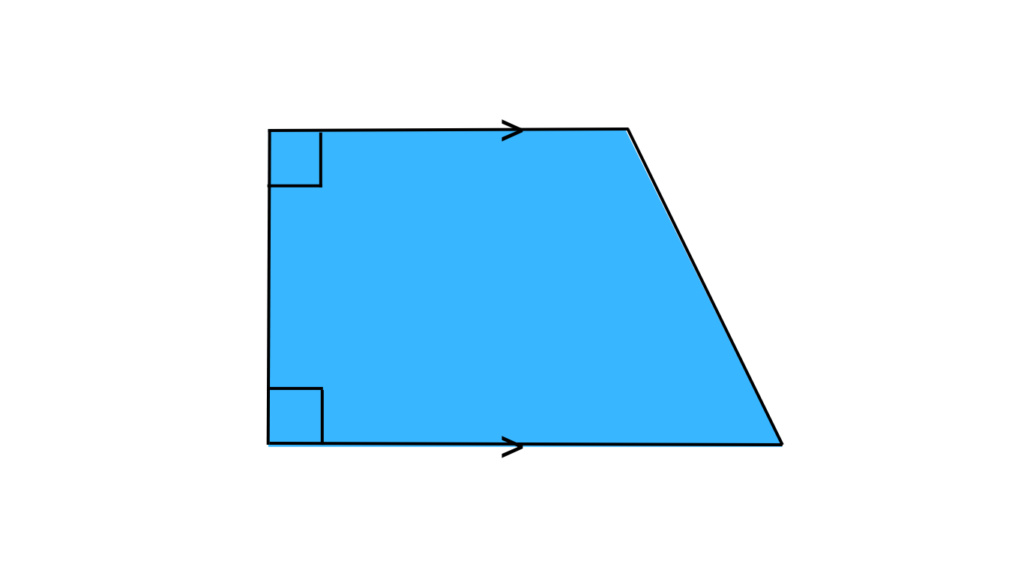
• Right Trapezoid: This trapezoid takes things a step further. One of its angles is a perfect right angle (think 90 degrees), just like the corner of a book. This makes it a cool combination of a rectangle (with its right angle) and a regular trapezoid. Picture an L-shaped roof – that’s a right trapezoid in action.

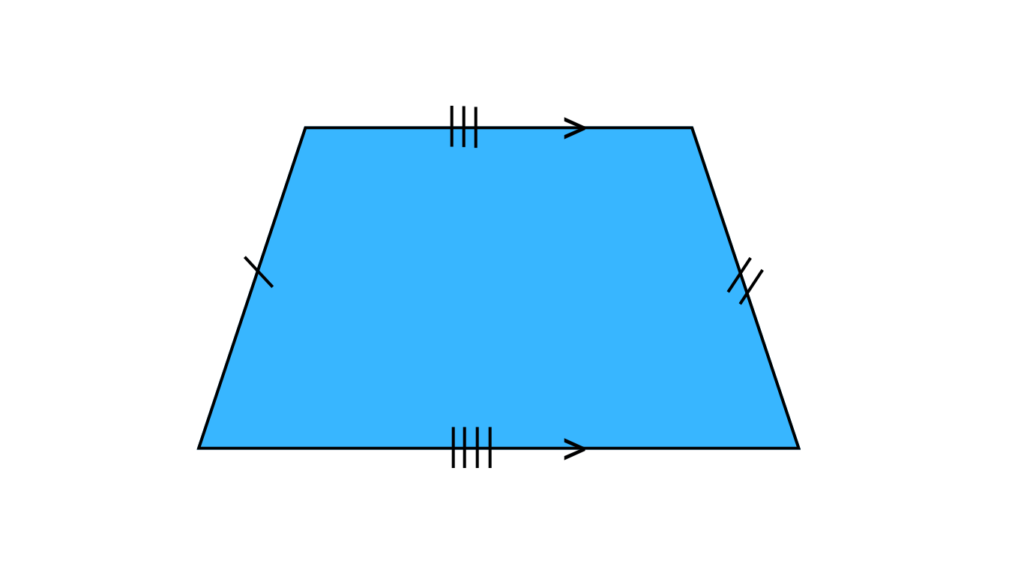
• Scalene Trapezoid: This is the most general type of trapezoid, where neither the legs nor the base angles are equal. It’s like the wild card of the trapezoid family, offering more variety in its shape.

Calculating the Area and Perimeter of a Trapezoid

After learning all the basic concepts of what is a trapezoid and its various, it is time to learn the concept of calculating the area and the perimeter of a trapezoid. So, the area of a trapezoid can be calculated using the formula:

Area of Trapezoid = 1/2 x (Base 1 + Base 2) x height

By plugging in the values of the bases and height into the formula, you can easily determine the area of a trapezoid.

Similarly, to calculate the perimeter of a trapezoid, we use the formula:

Perimeter of Trapezoid = Base 1 + Base 2 + Leg 1 + Leg 2

Let’s put this formula to the test! Say you have a trapezoid with a base of 10 cm, another base of 6 cm, a height of 8 cm, and legs of 3 cm and 5 cm. Here’s how to find the area and perimeter:

Area = (1/2) * (10 cm + 6 cm) * 8 cm

Area = (1/2) * (16 cm) * 8 cm

Area = 64 cm²

There you have it! Your trapezoid has an area of 64 square centimeters.

Perimeter = 10 cm + 6 cm + 3 cm + 5 cm

Perimeter = 24 cm

Therefore, the perimeter of the trapezoid is 24 centimeters.

Role of Trapezoids in Mathematics

Trapezoids play a significant role in geometry and mathematics:

• Geometric Concepts: Trapezoids are used to illustrate concepts like parallel lines, angles, and area calculations.
• Mathematical Formulas: The formula for the area of a trapezoid is a fundamental concept in geometry and algebraic calculations.

Application of Trapezoids in Daily Life Scenarios

While trapezoids may seem like abstract shapes, they have practical applications in everyday life:

• Architecture: Trapezoids are fundamental building blocks in many architectural designs. Think of the A-frame roofs of cabins, the slanted sides of bridges, or even the support structures for staircases. Their strength and stability make them a popular choice for various structures.
• Carpentry: Carpenters often work with trapezoidal pieces of wood when constructing furniture or frames.
• Engineering: From the wings of airplanes to the treads of stairs, trapezoids play a crucial role in engineering design. Their ability to distribute weight evenly and create strong support systems make them essential for building safe and functional structures.

How to Identify a Trapezoid

Visual Identification

To identify a trapezoid, look for a four-sided shape with one pair of parallel sides. This key feature sets trapezoids apart from other quadrilaterals.

Using Geometric Tools

A ruler and a protractor can help confirm whether a shape is a trapezoid. Measure the sides to check for parallelism and use the protractor to verify the angles.

Conclusion

So, there you have it! Through this exploration of what is a trapezoid, we have uncovered the definition, properties, and significance of this geometric figure. From understanding its unique characteristics to applying its area calculation formula, trapezoids offer a rich landscape for exploration in geometry and problem-solving. 

Recap of Key Points Covered in the Article:

• We defined what is a trapezoid and explored its key properties, including parallel bases, non-parallel sides, and height.
• We discussed the importance of calculating the area of a trapezoid and its applications in mathematics and real-life scenarios.
• We highlighted the role of trapezoids in mathematical concepts and problem-solving, emphasizing their practical significance.
• We provided strategies for recognizing trapezoids and reinforced learning through practice exercises.
• We demonstrated how the properties of trapezoids can be applied in practical examples to solve everyday problems.

Exploring the world of trapezoids opens up a realm of geometric possibilities and challenges. As you continue your journey in mathematics and geometry, remember the versatility and importance of understanding what is a trapezoid.

Frequently Asked Questions (FAQs)

What is a trapezoid in simple terms?

A trapezoid is a four-sided quadrilateral with one pair of parallel sides.

How can I determine if a shape is a trapezoid?

A shape is considered a trapezoid if it has one pair of parallel sides. The other two sides may have different lengths, but the presence of parallel bases is the defining characteristic of a trapezoid.

What is the formula for calculating the area of a trapezoid?

The formula for the area of a trapezoid is Area = 1/2 x (sum of bases) x height. By plugging in the values of the bases and height, you can easily find the area of a trapezoid.

Are trapezoids commonly used in real-world applications?

Yes, trapezoids have practical applications in various fields such as architecture, carpentry, and engineering. Understanding the properties of trapezoids can aid in designing structures, calculating material requirements, and solving geometric problems.