Introduction
Angles are the building blocks of geometry, and among them, adjacent angles stand out as the angles next door, sharing a common side and vertex. Just as neighbors interact and influence each other, adjacent angles play a crucial role in determining geometric relationships and solving various problems in mathematics.
This article will serve as your comprehensive guide to understanding adjacent angles. We will explore their definitions, properties, and applications in geometry, equipping you with the knowledge and skills to master these angles like a pro. Whether you’re a student looking to ace your geometry class or someone interested in exploring the fascinating world of angles, this article is for you.
What Are Adjacent Angles?
Let’s begin with the basics. Adjacent angles are two angles that share a common vertex and a common side but do not overlap. Imagine standing at a street corner where two roads meet. The angles formed on either side of the corner are adjacent. In simple terms, adjacent angles are neighbors—they share a boundary and are next to each other.
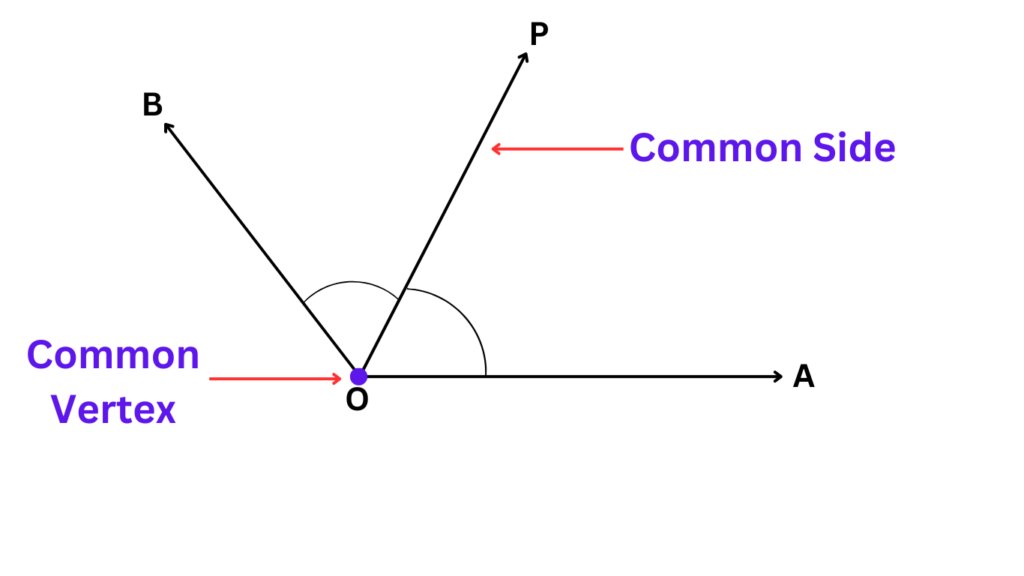
Characteristics of Adjacent Angles
- Common Vertex: Both angles originate from the same point.
- Common Side: They share one of their sides.
- No Overlap: While they share a side and a vertex, they do not overlap each other.
To visualize this, think of the hands of a clock at 3 o’clock. The angle between the minute hand and the hour hand is an adjacent angle to the angle on the other side of the hour hand. Simple, right?
Properties of Adjacent Angles
Now that we know what adjacent angles are, let’s explore their properties. These properties are essential for solving various geometric problems and understanding the relationships between angles.
Sum of Angles
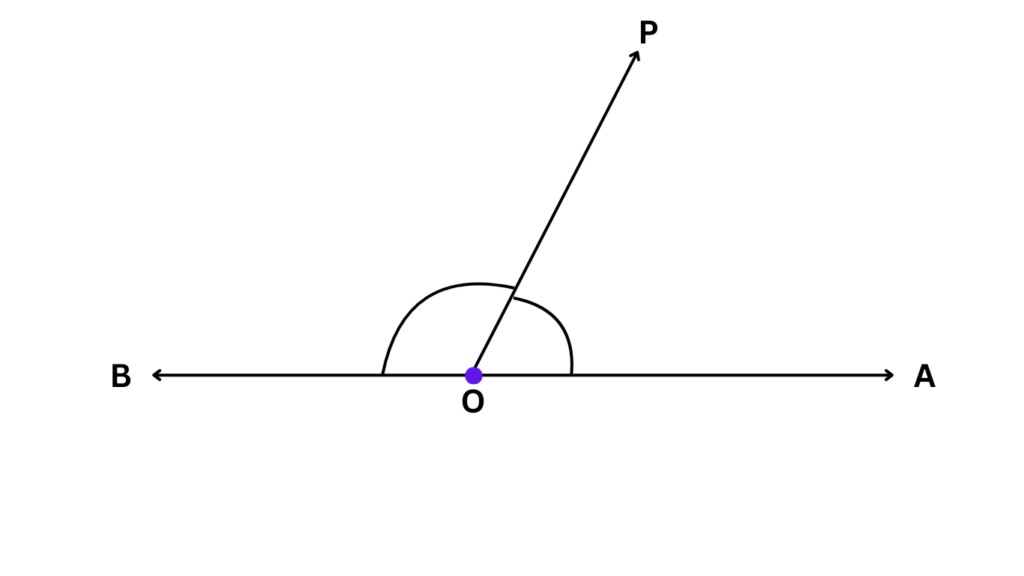
In some cases, adjacent angles can form a special pair known as a linear pair. A linear pair is a pair of adjacent angles whose non-common sides form a straight line. The sum of the angles in a linear pair is always 180 degrees. This property is handy when you need to find unknown angles.
Relationship with Complementary and Supplementary Angles
Adjacent angles can also be related to complementary and supplementary angles:
- Complementary Angles: Two angles are complementary if their sum is 90 degrees. Adjacent angles can be complementary, forming a right angle.
- Supplementary Angles: Two angles are supplementary if their sum is 180 degrees. In the case of a linear pair, adjacent angles are always supplementary.
Understanding these relationships helps in solving problems where angles need to be calculated based on given conditions.
Real-Life Examples
Adjacent angles are not just confined to your geometry homework. They play a crucial role in various fields and can be seen all around us.
Everyday Examples
- Corners of a Book: When you look at the corner of a book, the angles formed on either side of the corner are adjacent.
- Intersecting Roads: The angles formed by intersecting roads are adjacent.
- Clock Hands: The angles formed by the hands of a clock are adjacent as the minute hand moves around the hour hand.
- Table Edges: At the corner of a rectangular table, the angles on either side of the corner are adjacent.
- Window Frames: The angles formed by the sides of a window pane at the corners are adjacent.
Importance in Different Fields
- Architecture: Architects use adjacent angles to design buildings and structures with precise angles and measurements. For instance, the angles at the corners of a room or the design of a pitched roof often have to be adjacent.
- Engineering: Engineers apply this adjacent concept of angles in constructing bridges, roads, and various mechanical parts. In the design of gears, the angles where gear teeth meet are adjacent.
- Art: Artists use the adjacent concept of angles to create perspective and dimension in their work. When drawing a three-dimensional object, understanding how angles meet at edges can enhance the realism of the piece.
- Interior Design: Interior designers use the adjacent concept of angles to plan spaces efficiently, ensuring that furniture and decor align harmoniously within a room. By recognizing and understanding these angles, professionals in these fields can create functional and aesthetically pleasing designs.
How to Identify Adjacent Angles
Identifying adjacent angles is a fundamental skill in geometry. Here’s a detailed guide to help you spot them in various shapes and figures.
Step-by-Step Guide
- Look for a Common Vertex: Start by finding a point where two angles originate. This common vertex is the meeting point of the angles.
- Check for a Common Side: Ensure that both angles share one of their sides. This common side acts as the boundary between the two angles.
- Confirm No Overlap: Verify that the angles do not overlap each other. Adjacent angles should be distinct and separate, sharing only the vertex and one side.
Other Identification Process
- Using Geometric Shapes: In geometric shapes like triangles, quadrilaterals, and polygons, look for pairs of angles that share a side. For instance, in a rectangle, each corner (vertex) forms two angles that are adjacent.
- Analyzing Intersecting Lines: When two lines intersect, they form four angles. Each pair of angles that share a common vertex and one of the intersecting lines as a side are adjacent. This scenario often appears in problems involving linear pairs.
- Practical Application: In real-life objects like books, tables, and windows, trace the edges to find angles that are adjacent. At each corner, the angles meeting are adjacent. This practical observation helps in visualizing adjacent angles beyond paper diagrams.
Visual Aids
- Diagrams: Simple diagrams of shapes with highlighted adjacent angles can aid understanding. Label the common vertex and side to emphasize their adjacency.
- Interactive Tools: Use geometry software or online tools that allow you to manipulate shapes and observe how adjacent angles form and change. Tools like GeoGebra can be particularly useful for visual learners.
By following these steps and using visual aids, you can confidently identify these angles in any context.
Adjacent Angles vs. Other Types of Angles
Adjacent angles are often confused with other types of angles. Let’s compare them to clear up any confusion.
Vertical Angles
Vertical angles are formed when two lines intersect. They are opposite each other and always equal. Unlike the angles that are adjacent, vertical angles do not share a common side or vertex.
Complementary Angles
Complementary angles add up to 90 degrees. They can be adjacent but are not necessarily so. For example, the angles in a right triangle are complementary but not adjacent.
Supplementary Angles
Supplementary angles add up to 180 degrees. Adjacent angles in a linear pair are always supplementary, but supplementary angles are not always adjacent.
Understanding these differences is crucial for solving geometry problems accurately.
Conclusion
Adjacent angles are a fundamental concept in geometry, crucial for understanding more complex geometric principles. From the corners of a book to the design of buildings, they are everywhere around us. By mastering the identification and properties of it, you can enhance your problem-solving skills and appreciate the beauty of geometry in the world.
So, next time you see intersecting roads or the hands of a clock, take a moment to appreciate the adjacent angles at play. Practice identifying them in your daily life, and you’ll soon become a geometry pro.
Frequently Asked Questions (FAQs)
What is the difference between adjacent and vertical angles?
Adjacent angles share a common vertex and side but do not overlap, while vertical angles are opposite each other when two lines intersect and are always equal.
Can adjacent angles be supplementary?
Yes, adjacent angles can be supplementary if they form a linear pair, adding up to 180 degrees.
Are adjacent angles always equal?
No, adjacent angles are not always equal. Their equality depends on the specific geometry of the situation.
One Comment
Comments are closed.