How to Find Area: Stop Guessing, Start Calculating Like a Champ (2024)

Have you ever struggled with figuring out how to find area to estimate paint for your room or calculate fabric needs for a tablecloth?

The answer lies in understanding a fundamental concept in mathematics: area. In this comprehensive guide, we’ll embark on a journey to explore how to find area for various shapes, transforming you into a master of measurement in no time.

What is an Area?

Imagine a flat surface, like a tabletop or a sheet of paper. The area of this surface refers to the amount of space it occupies. Think of it like a giant ruler that measures the “squareness” of that space. We use different units to measure area, such as square meters (m²), square feet (ft²), and square centimeters (cm²). The unit chosen depends on the context and the size of the area being measured.

Why is finding an area important? You’d be surprised at how often area calculations come in handy. From estimating paint for a room to calculating the size of a garden, understanding the area is a valuable skill for various DIY projects and everyday tasks.

Exploring Shapes: A Formula for Each Friend

Now that we understand what area is, let’s unlock the secrets of how to find area for different shapes. Each shape has its own special formula, like a unique recipe for calculating its area.

The Rectangular Ruler: How to Find Area of Rectangles

Rectangles are those friendly shapes with four straight sides and four right angles. Imagine a rectangular table – its length is the longer side, and its width is the shorter side. To find the area of a rectangle, we simply multiply its length by its width. Here’s the formula:

Area of a Rectangle = Length (L) x Width (W)

Let’s see this in action. Suppose your rectangular table has a length of 6 meters (m) and a width of 3 meters (m). How to find area that the tabletop occupies?

Area = 6 m x 3 m = 18 square meters (m²)

This means you’ll need 18 square meters of tablecloth to cover the entire surface of the tabletop.

Real-Life Example: Knowing how to find area of a rectangle is crucial when buying carpets, flooring materials, or even wallpaper. By measuring the length and width of your room (in meters or feet), you can calculate the area and buy the exact amount of material needed.

The Square Squad: A Special Case of Rectangles

Squares are a special type of rectangle where all four sides are equal in length. Finding the area of a square is even simpler because we only need to know the length (or width) of one side. Here’s the formula:

Area of a Square = Side (S) x Side (S)

Let’s say you have a beautiful square rug with a side length of 2 meters (m). What’s the area it covers?

Area = 2 m x 2 m = 4 square meters (m²)

Real-Life Example: Squares come in handy for various purposes, like designing square tiles for a bathroom floor or calculating the area of a framed artwork.

The Triangle Trio: A Formula with a Twist

Triangles are those three-sided shapes that can come in various shapes and sizes. However, to find their area, we need a special formula that involves both their base and height. The base is any straight side of the triangle, and the height is the perpendicular distance from a vertex (corner) to the opposing base. Here’s the formula:

Area of a Triangle = 1/2 x Base (B) x Height (H)

Important Note: Make sure you identify the correct base and height for your specific triangle.

Let’s solve an example. Imagine a right-angled triangle with a base of 5 centimeters (cm) and a height of 3 centimeters (cm). How to find area of this right-angled triangle?

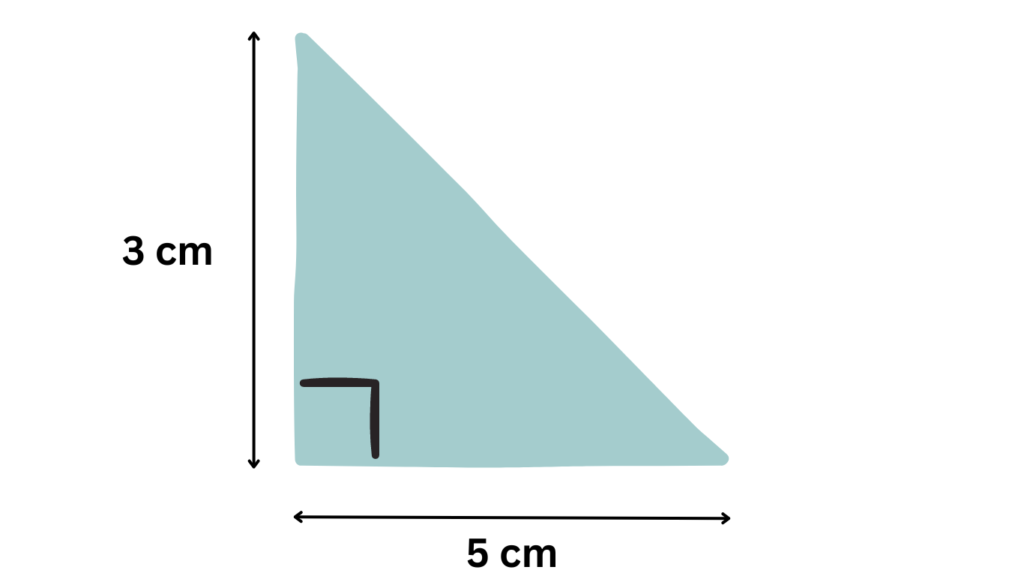
Area = 1/2 x 5 cm x 3 cm = 7.5 square centimeters (cm²)

Real-Life Example: Understanding how to find area of the triangles is useful for calculating the size of roof sections, triangular flower beds, or even slices of pizza (assuming they’re perfectly triangular, of course).

The Circle Club: Round and Rolling with Area

Circles are those friendly shapes with no corners and a single, continuous curved edge. Unlike shapes with straight sides, finding the area of a circle involves a special number called pi (π), which is approximately equal to 3.14. Here’s the formula:

Area of a Circle = π x Radius² (R²)

The radius (R) is the distance from the center of the circle to any point on its edge.

Let’s say you have a delicious round pizza with a radius of 10 centimeters (cm). How to find area of the pizza (i.e. the amount of space it covers)?

Area ≈ 3.14 x 10 cm x 10 cm ≈ 314 square centimeters (cm²) (Remember, pi is an approximation)

Real-Life Example: Finding the area of circles is essential in various fields, from calculating the size of round cakes and pizzas to designing circular gears or wheels.

The Trapezoid Troop: A Shape with Two Parallel Sides

Trapezoids are interesting shapes with four sides, where one pair of opposite sides is parallel. To find the area of a trapezoid, we use a formula that considers both bases and the height. Here’s the formula:

Area of a Trapezoid = 1/2 (Base₁ + Base₂) x Height (H)

Base₁ refers to the longer of the two parallel sides, and Base₂ refers to the shorter parallel side.

Imagine a trapezoid-shaped rooftop with a longer base of 8 meters (m), a shorter base of 6 meters (m), and a height of 4 meters (m). How to find area of the rooftop?

Area = 1/2 (8 m + 6 m) x 4 m = 7 x 4 m² = 28 square meters (m²)

Real-Life Example: Knowing how to find area of a trapezoid is useful for calculating the size of slanted roofs, garden beds with angled sides, or even certain types of tabletops.

Conquering Complex Shapes

We’ve tackled rectangles, squares, triangles, circles, and trapezoids, but the world of shapes is full of surprises. Sometimes, you might encounter shapes that are a combination of these simpler ones, or shapes with irregular curves. Here’s how to find area even in these scenarios:

A. Breakdown of Irregular Shapes into Simpler Components:

Imagine a shape with several curved edges or a combination of straight and curved sides. The trick here is to break it down into familiar shapes whose areas you already know how to find. For instance, consider a piece of land with a curved coastline. We can approximate the coastline by dividing it into smaller straight-line segments, creating a series of trapezoids. By calculating the area of each individual trapezoid and adding them all together, we can estimate the total area of the land.

B. Combining Different Formulas for Composite Figures:

Sometimes, a shape might be a combination of two or more of the shapes we’ve already explored. For example, a house floor plan might be a rectangle with a square cutout for a closet. To find the total area of the floor plan, we can calculate the area of the entire rectangle and then subtract the area of the square cutout. This involves using the formulas for both rectangles and squares.

These techniques are valuable for architects and interior designers who need to calculate the usable area of rooms with irregular shapes or built-in features.

Want to see these strategies in action? Okay! Let’s Solve a Problem.

Imagine a rectangular garden with a semi-circular pond at one end, as illustrated below:

• The rectangle has a length of 10 meters (m) and a width of 5 meters (m).
• The semi-circular pond has a radius of 2 meters (m).

Now, how to find area of this rectangular garden with the pond?

Step 1: Find the Area of the Rectangle

Area of rectangle = L x W = 10 m x 5 m = 50 square meters (m²)

Step 2: Find the Area of the Semi-circle

We know the formula for the whole circle: Area of circle = π x R². However, we only have half the circle here. The area of a semi-circle is half the area of the whole circle.

Area of semi-circle = 1/2 (π x R²)

Step 3: Calculate the Area of the Semi-circle

Area of semi-circle = 1/2 (3.14 x 2 m x 2 m) ≈ 6.28 square meters (m²) (round to two decimal places)

Step 4: Find the Total Area of the Garden

The total area of the garden is the area of the rectangle minus the area of the semi-circular pond.

Total Area = Area of the rectangle – Area of the semi-circle

Total Area = 50 m² – 6.28 m² ≈ 43.72 square meters (m²) (round to two decimal places)

Therefore, the total usable area of the garden is approximately 43.72 square meters.

Avoiding the Pitfalls: Common Mistakes and How to Dodge Them

Understanding how to find area is a valuable skill, but it’s important to be aware of some common mistakes that can creep in. Here’s how to avoid these pitfalls and ensure accurate area calculations:

A. Identification of Typical Errors Made in Area Calculations

• Mixing Up Units: Make sure you use consistent units throughout your calculations. Don’t mix meters with centimeters or feet with inches. Convert everything to the same unit before applying the formula.
• Incorrect Base and Height: Especially in triangles, ensure you identify the correct base and height. The height is always perpendicular to the base you choose.
• Forgetting Pi (π) for Circles: Remember to include pi (π) when calculating the area of circles. You can use the value 3.14 or rely on your calculator’s pi function.
• Misinterpreting Shape Properties: Not all rectangles are squares! Double-check the properties of the shape before applying the corresponding formula.

B. Tips to Avoid Common Misconceptions and Improve Accuracy

• Double-Check Measurements: Ensure your measurements are accurate before plugging numbers into formulas. A small measurement error can lead to a significant difference in the calculated area.
• Draw Diagrams: Sketching a diagram of the shape can help visualize the base, height, radius, or other relevant measurements needed for the formula.
• Practice Makes Perfect: The more you practice finding areas for different shapes, the more comfortable and accurate you’ll become.
• Use Online Resources: Many online calculators and tutorials are available to help you with specific shapes or complex area problems.

By following these tips and avoiding common mistakes, you can easily tackle the problem of how to find area and you’ll be well on your way to becoming an area calculation pro.

Putting it All Together: Applying Your Knowledge

Ready to test your area mastery? Let’s solve some engaging word problems that involve finding area for different shapes:

Problem 1: The Rectangular Rooftop Challenge

Imagine a rectangular rooftop with a length of 8 meters (m) and a width of 6 meters (m). There’s a square chimney right in the middle, with a side length of 2 meters (m). You need to calculate the area of the rooftop excluding the chimney, as you won’t be painting that part.

Solution:

1. Find the area of the entire rectangle: Area of rectangle = L x W = 8 m x 6 m = 48 square meters (m²)
2. Find the area of the square chimney: Area of square = S x S = 2 m x 2 m = 4 square meters (m²)
3. Calculate the area of the rooftop excluding the chimney: Total Area – Area of chimney = 48 m² – 4 m² = 44 square meters (m²)

Therefore, the area you need to paint on the rooftop is 44 square meters.

Problem 2: The Triangular Flower Bed

You’re designing a beautiful triangular flower bed. The base of the triangle is 5 meters (m), and the height from the base to the opposite vertex is 3 meters (m). How much space do you have for planting flowers in your triangular bed?

Solution:

Remember the formula for a triangle: Area of triangle = 1/2 x Base x Height

So, Area of triangle = 1/2 x 5 m x 3 m = 7.5 square meters (m²)

The triangular flower bed has an area of 7.5 square meters, perfect for planting a variety of colorful flowers.

Conclusion

Congratulations! You’ve embarked on a journey to explore the fascinating world of the area and emerged victorious. You’ve learned the formulas of how to find area of rectangles, squares, triangles, circles, and trapezoids. You’ve discovered strategies for tackling complex shapes and avoiding common pitfalls. Most importantly, you’ve unlocked the power of applying area calculations to various real-world scenarios.

As you continue your exploration of mathematics, you’ll encounter even more fascinating concepts related to area. You might delve into the concept of volume, which extends the idea of area to three-dimensional shapes. You might explore the world of surface area, which calculates the total area of all the external faces of a 3D object.

The possibilities are endless! But for now, celebrate your mastery of area and get ready to apply this valuable skill in your everyday life!

Frequently Asked Questions (FAQ)

How to Find Area of a Triangle?

To find area of a triangle we will need the base and height of the triangle and after knowing these two components we will use the formula: Area of a Triangle = 1/2 x Base (B) x Height (H).

How to Find Area of a Circle?

To find area of a circle we will need the radius of the circle first then using the formula: Area of a Circle = π x Radius² (R²), we can the find the area easily.

How to Find Area of a Rectangle?

To find area of a rectangle we first determine the length and width of the rectangle then use the formula: Area of a Rectangle = Length (L) x Width (W) and find the area of a rectangle.

How to Find Area of a Trapezoid?

To find area of a trapezoid we first determine two bases and the height of trapezoids then use the formula: Area of a Trapezoid = 1/2 (Base₁ + Base₂) x Height (H) and find the area of a trapezoid.