Are you wondering why should you learn how to find volume? Is it even going to help you in the real world or would you even use it in life?
The simple answer is yes. Learning how to find volume will help you in the real world to tackle various problems and you will need it in life. So, how does it you ask? Have you ever stared at a can of paint, wondering how much it would take to cover your living room walls? Or perhaps you’ve meticulously measured the ingredients for a cake recipe, only to realize you forgot to consider the size of your baking pan. These situations, and countless others in everyday life, involve understanding how to find volume.
But fear not, fellow adventurer in the world of 3D space! This guide will equip you with the knowledge and tools to conquer the concept of volume with confidence.
What is Volume?
Imagine a shoebox. Unlike its flat cardboard surface (which is its area), the shoebox has a volume. Volume refers to the amount of three-dimensional space an object occupies. Simply put, it’s a measure of how much “stuff” can fit inside that object.
Here’s where volume differs from its two-dimensional cousin, area. Area tells you how much space an object covers on a flat surface, like the length and width of your rectangular rug. Volume, on the other hand, takes height into account, giving you a sense of the object’s overall “bigness” in 3D.
Why is Finding Volume Important?
Believe it or not, finding volume is a crucial skill in many aspects of life. From the seemingly mundane to the awe-inspiring, here are just a few examples:
- Construction: Architects and engineers rely on volume calculations to determine the amount of concrete needed to build a foundation or the capacity of a water tank.
- Cooking: Bakers use volume measurements (like cups and teaspoons) to ensure their recipes come out perfectly.
- Science Experiments: Whether measuring the volume of a liquid in a test tube or calculating the air displaced by a balloon, volume plays a key role in scientific exploration.
- Packing and Shipping: Ever tried to cram too much into a suitcase before a trip? Understanding volume helps you estimate how much stuff you can fit in a box or container before it overflows.
- Medicine: Doctors might use volume measurements to determine the dosage of medication for a patient.
As you can see, how to find volume is a valuable tool across various disciplines.
Unveiling the Formula: How to Find Volume
Now that we understand the concept of volume, it’s time to equip ourselves with the magic formula that unlocks its calculation. Our first adventure will focus on the rectangular prism, a familiar shape with a flat, rectangular base and perpendicular sides. Think of a shoebox, a tissue box, or even your phone.
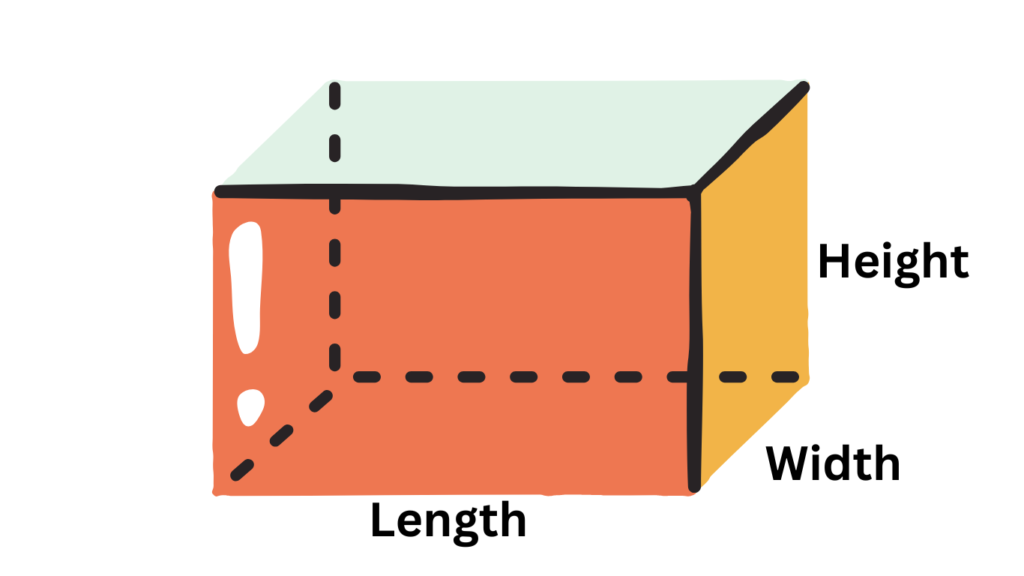
The secret formula for finding the volume of a rectangular prism is:
V = l x w x h
Here’s a breakdown of this mighty formula:
- V: This represents the volume of the rectangular prism, measured in cubic units (like cubic centimeters or cubic meters).
- l: This stands for the length of the prism’s base. Imagine the longest side of the shoebox.
- w: This represents the width of the base. Think of the shorter side opposite the length.
- h: This signifies the height of the prism. This is the distance from the base of the shoebox to its top.
Important Note: The order in which you multiply these values (l x w x h) doesn’t matter. As long as you use the correct measurements for each variable, you’ll get the correct volume!
Units of Measurement: Keeping Things Consistent
Just like you wouldn’t measure your height in teaspoons, it’s crucial to use consistent units when finding volume. Here are some common units for volume:
- Cubic centimeters (cm³): Often used for smaller objects.
- Cubic meters (m³): Ideal for larger objects or volumes of liquids.
- Liters (L): Another common unit for liquids, equivalent to 1 cubic decimeter (dm³).
Converting Between Units: Sometimes, you might encounter measurements in different units. Don’t worry! Conversion factors can help you switch between units seamlessly. For example, there are 1000 cubic centimeters in 1 cubic meter.
Remember: Always make sure your units are consistent throughout the calculation to ensure an accurate result.
Conquering Different Shapes
So far, we’ve mastered the rectangular prism, but the world of 3D shapes is much more diverse. Let’s explore some common shapes and unlock the secrets of finding their volumes.
Beyond Rectangles: A Formula for Every Form
- Cube: This champion of uniformity has all its sides equal in length. Finding the volume of a cube is a breeze with this formula:
V = s³
Here, “s” represents the length (or width, or height) of any side of the cube, since all sides are the same. Imagine a perfectly shaped Rubik’s cube – all its sides are equal, making volume calculation a snap.
- Cylinder: Picture a soup can or a tall vase. Cylinders have a circular base and a flat top, with a straight side connecting them. To find the volume of a cylinder, we need a new friend: pi (π), a mathematical constant roughly equal to 3.14. Here’s the formula:
V = πr²h
Here, “r” represents the radius of the cylinder’s circular base. Think of it as the distance from the center of the base to its edge and “h” signifies the height of the cylinder, just like in a rectangular prism.
- Cone: Ice cream cones and party hats are classic examples of cones. They have a circular base, a pointed tip (called the apex), and a slanted side. The formula for finding the volume of a cone is:
V = (1/3)πr²h
Here, “r” and “h” have the same meaning as in the cylinder formula. The factor of (1/3) accounts for the cone’s pointy shape, allowing us to calculate its enclosed space accurately.
- Sphere: Basketballs, globes, and marbles are all spheres. These perfectly round shapes have a formula all their own:
V = (4/3)πr³
In this formula, “r” represents the radius of the sphere, similar to the cylinder. The factor of (4/3) and the exponent of 3 account for the sphere’s unique three-dimensional roundness.
Putting It into Practice
With a solid understanding of volume formulas and units, let’s embark on some real-world adventures in volume calculation. We’ll tackle different shapes, putting our newfound knowledge to the test.
Conquering the Rectangular Prism
Imagine you’re revamping your living room and need to buy paint. The room measures 6 meters long, 4 meters wide, and 3 meters high. How much paint do you need to cover the walls, assuming one can of paint covers 10 square meters?
Step 1: Identify the Shape and Formula
This scenario involves a rectangular prism (your room). We’ll use the formula V = l x w x h.
Step 2: Plug in the Values
V = 6 m (length) x 4 m (width) x 3 m (height) V = 72 cubic meters
Step 3: Interpret the Result
The volume of your room is 72 cubic meters. However, paint covers an area, not volume. Here’s a trick: since you only need paint for the walls, consider the walls as giant rectangles themselves. Multiply the room’s length and height (since walls typically go from floor to ceiling) to find the total wall area.
Area of one wall = 6 m (length) x 3 m (height) = 18 square meters
Since you have four walls, the total wall area to be painted is:
Total wall area = 18 m² (area of one wall) x 4 walls = 72 square meters
Step 4: Considering Paint Coverage
One can of paint covers 10 square meters, and you need to cover 72 square meters. Therefore:
Number of paint cans needed = 72 square meters (total wall area) / 10 square meters (coverage per can) = 7.2 cans
Since you can’t buy parts of cans, round up to 8 cans of paint. This ensures you have enough to cover the walls with a single coat.
See how understanding volume helped us not only calculate the room’s space but also determine the amount of paint needed – a valuable skill for any DIY enthusiast.
Unwrapping the Volume of Round Containers
Cylinders are all around us, from the humble soup can to the majestic water tower. Let’s use our newfound knowledge of how to find volume of the cylinder formula (V = πr²h) to tackle some cylindrical challenges.
Calculating the Volume of Punch in a Juice Dispenser
Imagine you’re hosting a party and need to know how much punch to prepare. Your trusty juice dispenser is cylindrical, with a base diameter of 20 centimeters and a height of 30 centimeters. How much punch can it hold?
Step 1: Identify the Shape and Formula
This scenario involves a cylinder (the juice dispenser). We’ll use the formula V = πr²h.
Step 2: Find the Radius
Remember, the formula requires the radius (r), not the diameter. The diameter is the distance across the circle at its widest point. The radius is half the diameter. Therefore:
r = diameter / 2 = 20 cm / 2 = 10 centimeters
Step 3: Plug in the Values
We know π is approximately 3.14, r is 10 cm, and h is 30 cm. Let’s substitute these values into the formula:
V = π (10 cm)² x 30 cm V ≈ 3.14 x 100 cm² x 30 cm V ≈ 3140 cubic centimeters
Step 4: Interpret the Result
The juice dispenser can hold approximately 3140 cubic centimeters of punch. However, it’s wise to leave some space at the top to avoid spills. Consider this a safety factor.
Cylindrical Fun Fact: Did you know that many party cups are also cylindrical? Using the same formula, you can calculate how much liquid each cup can hold.
Determining the Volume of Water in a Cylindrical Pool
Summer is here, and you’re eager to take a dip in your above-ground pool. The pool is cylindrical, with a diameter of 4 meters and a depth of 1.5 meters. How much water does it take to fill the pool completely?
Step 1: Identify the Shape and Formula
This scenario involves a cylinder (the pool). We’ll use the formula V = πr²h.
Step 2: Find the Radius
Following the same logic as before, the radius (r) is half the diameter:
r = diameter / 2 = 4 meters / 2 = 2 meters
Step 3: Plug in the Values
We know π is approximately 3.14, r is 2 meters, and h is 1.5 meters. Let’s substitute these values into the formula:
V = π (2 meters)² x 1.5 meters V ≈ 3.14 x 4 meters² x 1.5 meters V ≈ 18.84 cubic meters
Step 4: Interpret the Result
The pool can hold approximately 18.84 cubic meters of water. Remember, this is an ideal scenario. In reality, factors like splashing and uneven pool floors might influence the actual amount of water needed.
Therefore, we’ve successfully calculated the volume of punch and pool water, showcasing the versatility of the cylinder formula in real-world situations.
Unveiling the Volume of Pointed Shapes
Cones, with their distinctive pointed tips, add a touch of whimsy to the world of 3D shapes. From party hats to ice cream cones, understanding their volume can be quite useful. Let’s explore how to find volume of cones using the formula V = (1/3)πr²h.
Calculating the Volume of Ice Cream in a Cone
Imagine you’re at a birthday party and receive a delicious ice cream cone. The ice cream fills the cone to the top, and you’re curious about the volume of this sweet treat. The cone has a base diameter of 6 centimeters and a height of 8 centimeters. How much ice cream are you enjoying?
Step 1: Identify the Shape and Formula
This scenario involves a cone (the ice cream cone). We’ll use the formula V = (1/3)πr²h.
Step 2: Find the Radius
As before, the diameter needs to be converted to radius:
r = diameter / 2 = 6 cm / 2 = 3 centimeters
Step 3: Plug in the Values
We know π is approximately 3.14, r is 3 cm, and h is 8 cm. Let’s substitute these values into the formula:
V = (1/3)π (3 cm)² x 8 cm V ≈ (1/3) x 3.14 x 9 cm² x 8 cm V ≈ 76.19 cubic centimeters (rounded to two decimal places)
Step 4: Interpret the Result
You’re enjoying approximately 76.19 cubic centimeters of ice cream! Remember, this is an estimate, and the actual amount might vary depending on how the cone is filled.
Determining the Volume of Popcorn in a Cone-Shaped Hat
Party favors often come in fun shapes, and sometimes those shapes are cones. Imagine a party hat shaped like a cone, filled with delicious popcorn. The hat has a base diameter of 10 centimeters and a height of 15 centimeters. How to find volume of the popcorn or say how much popcorn can it hold?
Step 1: Identify the Shape and Formula
This scenario involves a cone (the party hat). We’ll use the formula V = (1/3)πr²h.
Step 2: Find the Radius
Following the familiar pattern:
r = diameter / 2 = 10 cm / 2 = 5 centimeters
Step 3: Plug in the Values
We know π is approximately 3.14, r is 5 cm, and h is 15 cm. Let’s substitute these values into the formula:
V = (1/3)π (5 cm)² x 15 cm V ≈ (1/3) x 3.14 x 25 cm² x 15 cm V ≈ 125.66 cubic centimeters (rounded to two decimal places)
Step 4: Interpret the Result
The party hat can hold approximately 125.66 cubic centimeters of popcorn. This is a helpful estimate, but keep in mind that popcorn kernels have irregular shapes, and packing them efficiently might affect the actual volume.
Unveiling the Volume of Round Solids
Spheres, those perfectly round shapes, are all around us – from basketballs to marbles. Their volume calculation uses the formula V = (4/3)πr³, which might seem intimidating at first. However, with a step-by-step approach, we can conquer spheres too.
Determining the Volume of Air in a Basketball
Imagine you’re an aspiring basketball player and want to understand how to find volume of air a basketball holds. Your basketball has a diameter of 24 centimeters. How much air does it contain?
Step 1: Identify the Shape and Formula
This scenario involves a sphere (the basketball). We’ll use the formula V = (4/3)πr³.
Step 2: Find the Radius
Remember, the formula requires the radius, not the diameter. As before, the radius is half the diameter:
r = diameter / 2 = 24 cm / 2 = 12 centimeters
Step 3: Plug in the Values
We know π is approximately 3.14, and r is 12 cm. Let’s substitute these values into the formula:
V = (4/3)π (12 cm)³ V ≈ (4/3) x 3.14 x 1728 cm³ V ≈ 7238.4 cubic centimeters (rounded to one decimal place)
Step 4: Interpret the Result
The basketball can hold approximately 7238.4 cubic centimeters of air. In reality, the internal components like the bladder might occupy some space, so the actual air volume might be slightly less.
Calculating the Volume of Water in a Beach Ball
Summer wouldn’t be complete without a beach ball! Imagine a giant beach ball with a diameter of 1 meter. If you fill it completely with water, how much water will it hold?
Step 1: Identify the Shape and Formula
This scenario involves a sphere (the beach ball). We’ll use the formula V = (4/3)πr³.
Step 2: Find the Radius
Following the usual conversion:
r = diameter / 2 = 1 meter / 2 = 0.5 meters (since we’re working with meters, not centimeters)
Step 3: Plug in the Values
We know π is approximately 3.14, and r is 0.5 meters. Let’s substitute these values into the formula:
V = (4/3)π (0.5 meters)³ V ≈ (4/3) x 3.14 x 0.125 m³ V ≈ 0.523 cubic meters (rounded to three decimal places)
Step 4: Interpret the Result
The beach ball can hold approximately 0.523 cubic meters of water. This is a significant amount, so be prepared for a refreshing splash when you toss it around!
Conclusion
We’ve embarked on a fantastic journey, exploring the concept of volume, unlocking formulas for various shapes, and putting them into practice with real-world examples. The ability how to find volume is a valuable skill applicable in countless fields. From everyday tasks to scientific endeavors, understanding 3D space opens doors to exciting possibilities.
So, the next time you face the question of how to find volume, remember the formulas, conquer those calculations, and celebrate your newfound knowledge. The world of 3D awaits your exploration.
Frequently Asked Questions (FAQs)
How to Find Volume of a Rectangular Prism?
We can find the volume of a rectangular prism by multiplying the length, width, and height of the prism. i.e. Volume of a Rectangular Prism = Length x Width x Height
How to Find Volume of a Cylinder?
To find the volume of a cylinder, we will first need to determine its radius and height and then use the formula: V = πr²h to get the volume.
How to Find Volume of a Cone?
To find the volume of a cone, we will first need to determine its radius and height and then use the formula: V = (1/3)πr²h to get the volume.
How to Find Volume of a Sphere?
To find the volume of a sphere, we will first need to determine its radius and then use the formula: V = (4/3)πr³ to get the volume.