Imagine playing a game where you connect dots to create a perfect shape. Every connection you make is called a line segment. This simple yet powerful concept forms the foundation of geometry and plays a vital role in various fields, from art and design to architecture and engineering. In this article, we will explore its fascinating world, delving into its definition, properties, types, real-world applications, and more. By the end of this journey, you’ll have a comprehensive understanding of them and their significance in our everyday lives.
What is a Line Segment?
Let’s start with the basics. A line segment is a part of a line that is bounded by two distinct endpoints. Unlike a line that extends infinitely in both directions, they have a definite start and end. This means it is measurable and can be used to define shapes, distances, and structures.
Imagine a line – a perfectly straight path stretching endlessly in both directions. Now, pinch that line at two specific points. Those pinched sections, marked by distinct dots, are our line segments. They’re like tiny slices of a long, endless line, with a definite beginning and end.
Here’s a helpful visual to solidify the concept:
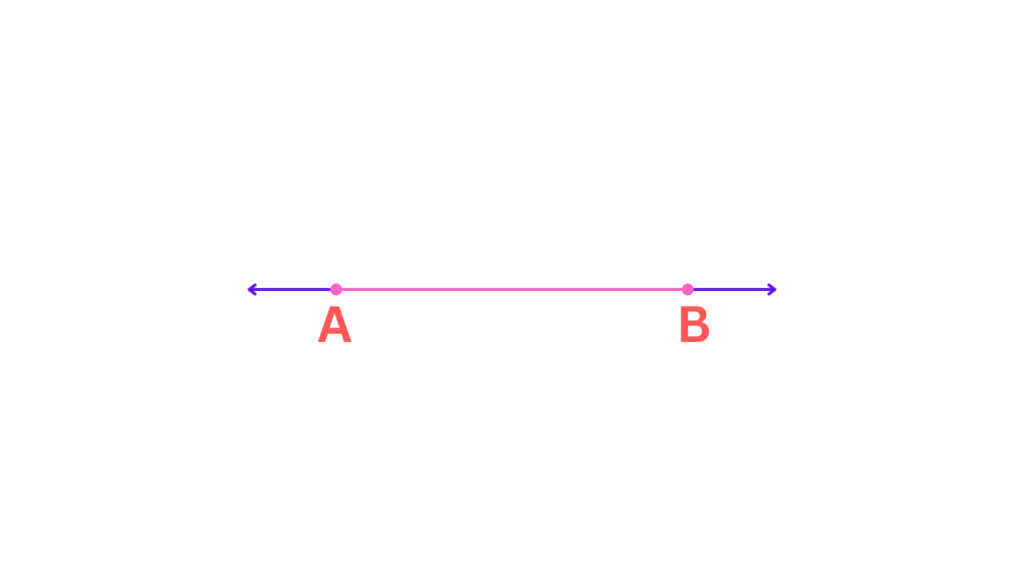
See how they have clear endpoints (marked A and B). These distinct points define the length of the line segment, making it a finite piece of a much larger, infinite line.
Properties of Line Segments
Now that you know the basic definition, let’s delve into its key properties:
- Fixed Length
One of the primary characteristics is its fixed length. This is the most crucial aspect. Unlike a line that extends forever, they have a definite length that can be measured. This makes it a useful tool for measuring distances and creating precise geometric shapes. For example, if you want to draw a triangle with specific side lengths, you would use those lengths. Similarly, you can use a ruler, a pencil, or even your finger to measure the distance between the two endpoints.
- Mark Those Endpoints:
Remember the two distinct dots marking the beginning and end of a line segment? Those aren’t just decorations; they’re essential! These endpoints define the specific portion of the line we’re considering. If not these endpoints, it would be called a line.
- Measurement
To measure a line segment, you simply measure the distance between its two endpoints. This can be done using a ruler in a physical setting or using the distance formula in a coordinate system. Accurate measurement is crucial in fields like engineering and construction, where precision is key.
- Midpoint
The midpoint of a line segment is the point that divides the segment into two equal parts. It is found exactly halfway between the endpoints. Suppose the endpoints of AB are given by coordinates (x1, y1) and (x2, y2), the midpoint M is calculated as:
M = [(x1 + x2)/2, (y1 + y2)/2]
The midpoint is useful in various applications, such as finding the center of a line segment or creating symmetrical designs.
Line Segments vs. Line vs. Ray
Ah, the age-old confusion – line segments vs. lines vs. Ray. Don’t worry, you’re not alone. Here’s the key difference:
- Line vs. Line Segment
A common misconception is that a line and a line segment are the same. However, a line extends infinitely in both directions, while a line segment has definite endpoints and a fixed length. Understanding this difference is crucial for accurate geometric analysis.
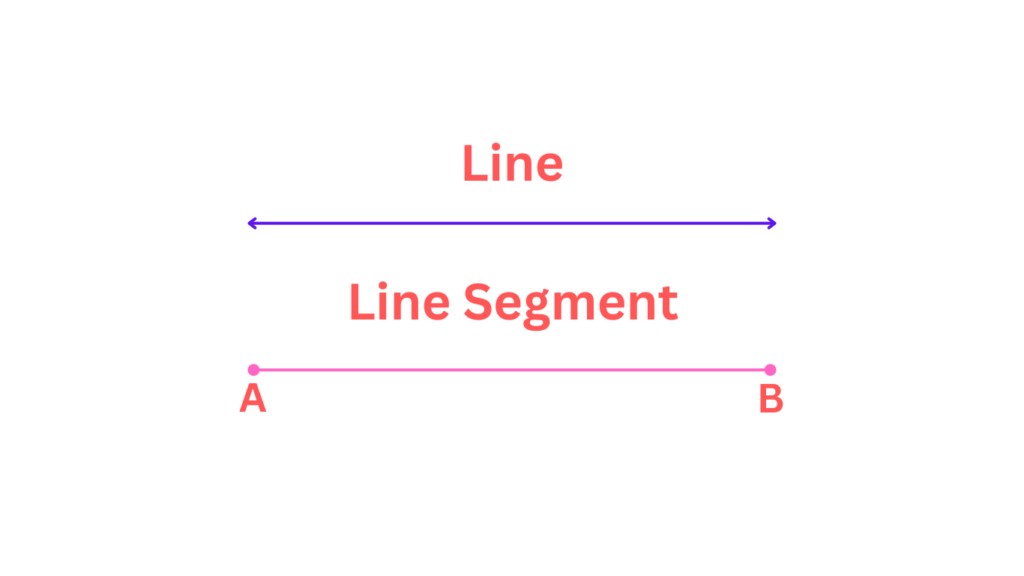
Imagine a line segment as a specific road trip you’re taking. You have a starting point (your hometown) and an ending point (your destination). The road between those two points is your line segment, with a clear beginning and end. Lines, on the other hand, are like endless highways. They stretch on forever in both directions, with no starting or ending point. You can drive on a line forever (at least in theory!), never reaching a specific destination.
- Line Segment vs. Ray
Another misconception is confusing line segments with rays. A ray starts at one point and extends infinitely in one direction. In contrast, a line segment has two endpoints and does not extend infinitely. Recognizing this distinction helps in solving geometric problems correctly.
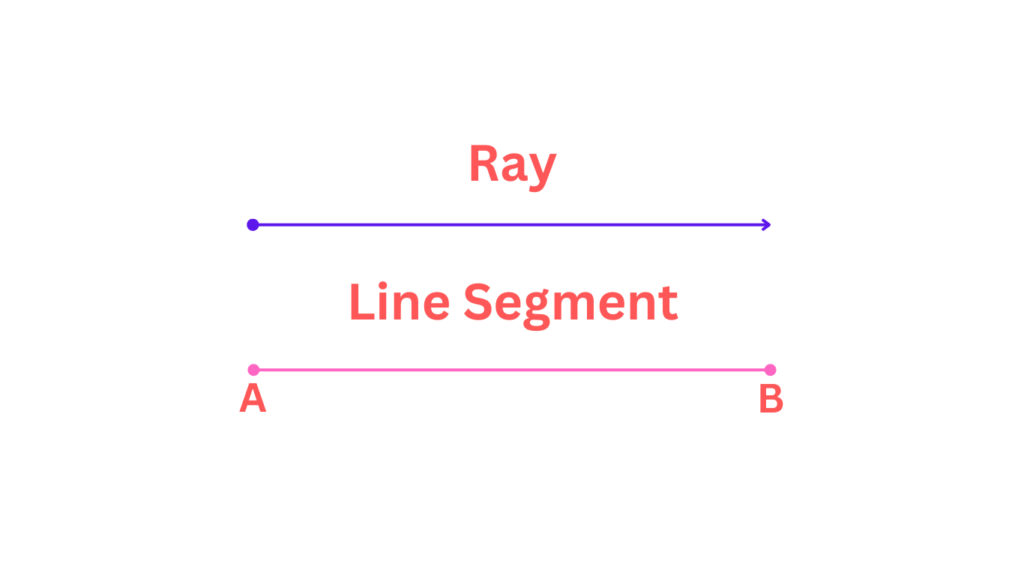
As discussed earlier, the line segment is a road trip with a clear beginning and a definite end. Now, picture a ray as a road trip with an exciting twist. You hop in your car, fueled by adventure, and hit the gas… but there’s no set destination. The road stretches endlessly in one direction, like a never-ending highway. You can keep driving forever (at least in theory!), with no specific endpoint in sight.
How to Draw
Among various things we have learned in this article, drawing these line segments accurately is a fundamental skill in geometry, art, and various practical applications. So, here is the step-by-step process of how to draw them correctly:
Firstly, you will need some tools to draw them. So, the tools you need are:
- Ruler: For drawing straight lines and measuring lengths.
- Pencil: For making precise marks.
- Graph Paper: For easy alignment and accuracy.
Now, after you have gathered all the tools required to draw this is how you do it:
Step 1: Mark the Endpoints – Use the ruler to mark the positions of the endpoints on the paper.
Step 2: Align the Ruler – Place the ruler so that it connects the two marked points.
Step 3: Draw the Line Segment – Use the pencil to draw a straight line between the endpoints, following the edge of the ruler. And there you have it! It is ready now.
Formulas Involving Line Segments
- Distance Formula
The distance formula is used to calculate the length of them in a coordinate plane. If the endpoints of the line segment AB are given by coordinates (x1, y1) and (x2, y2), the length ‘d’ is calculated as:
d = √(x2 – x1)^2 + (y2 -y1)^2
This formula is derived from the Pythagorean theorem and helps in finding its exact length.
- Midpoint Formula
As mentioned earlier, the midpoint of a line segment is the point that divides it into two equal parts. If the endpoints are (x1, y1) and (x2, y2), the midpoint M is given by:
M = [(x1 + x2)/2, (y1 + y2)/2]
This formula is essential in various geometric constructions and analyses.
Real-World Applications
Line segments are not just abstract concepts; they have numerous practical applications in our daily lives. Here are some examples:
- Architecture and Engineering
In architecture and engineering, they are used to design and construct buildings, bridges, and other structures. They help in defining dimensions, creating floor plans, and ensuring that components fit together accurately. For instance, the beams and columns in a building are designed using this concept and it is to maintain structural integrity.
- Urban Planning and Road Design
Urban planners use them to design efficient road networks and city layouts. Streets and avenues are often laid out in a grid pattern, with parallel lines ensuring organized traffic flow and accessibility. They help in creating clear and precise maps, improving navigation and safety.
- Art and Design
Artists and designers use them to create balance, symmetry, and proportion in their work. Whether it’s a painting, sculpture, or digital design, they help define shapes and patterns. For example, in perspective drawing, they are used to create the illusion of depth and distance.
- Everyday Objects
They are all around us in everyday objects. The edges of a piece of paper, the sides of a book, legs of the table, and the lines on a ruler are all examples of line segments. These segments help in defining shapes and providing structure to objects we use daily.
Parallel and Perpendicular Line
Understanding the relationship between line segments is crucial in geometry. Two important relationships are parallelism and perpendicularity.
- Parallel Line
Parallel lines are two or more line segments that never intersect and remain equidistant from each other. They have the same slope in a coordinate plane. For example, the opposite sides of a rectangle are parallel lines.
- Perpendicular Line
Perpendicular lines (formed by line segments) intersect at a right angle (90 degrees). They form an “L” shape and their slopes are negative reciprocals of each other. For instance, the sides of a square are perpendicular to each other.
- Intersection Points
When line segments intersect, they form various angles and shapes. The point where they intersect is called the intersection point also commonly called as point of intersection. Understanding these intersections helps in solving geometric problems and creating complex designs.
Conclusion
Line segments are fundamental building blocks of geometry, with applications that extend far beyond the classroom. From constructing buildings to creating art, understanding them enhances our ability to navigate and shape the world around us. By mastering the concepts and properties of them, you gain valuable insights into the structure and design of everything from simple objects to complex systems. So, the next time you see a straight edge or a defined distance, you’ll appreciate the elegant simplicity of line segments and their vital role in our daily lives.
Frequently Asked Questions (FAQs)
What Are Line Segments in Geometry?
Line segments are parts of a line bounded by two distinct endpoints. They have a fixed length and are used to define shapes, distances, and structures.
How Do You Measure a Line Segment?
To measure a line segment, use a ruler to find the distance between its two endpoints. In a coordinate plane, use the distance formula: d = √(x2 – x1)^2 + (y2 -y1)^2.
What Is the Difference Between a Line Segment and a Line?
A line extends infinitely in both directions, while a line segment has two endpoints and a fixed length. The two endpoints is what really differentiates them. So, always look for endpoints to differentiate them.