Is Mixed Fraction making you go haywire? You are confused about whether these unusual-looking fractions are relevant in your life.
But have you ever stared at a recipe that called for 1 ¾ cups of flour and wondered, “Wait, how do I measure that?” Or maybe you’ve helped with a DIY project that required cutting a board into pieces that were 2 ½ feet long? Well, my friends, these situations are where the wonderful world of mixed fractions comes into play.
They might sound intimidating at first but fear not. They’re simply a combination of whole numbers and fractions, like slices of a delicious pie. Understanding these fractions is a key skill in arithmetic, and this comprehensive guide will equip you with all the knowledge and tricks to conquer them with confidence.
What are Mixed Fractions?
Imagine a delicious pie cut into eight slices. If you’ve eaten three whole slices, that’s represented by the number 3. But what if you also want a tiny sliver from the fourth slice? That sliver can be written as ¼. Combining the whole slices (3) and the leftover fraction (¼) gives us a mixed fraction, written as 3¼.
In simpler terms, a mixed fraction has two parts:
- Whole number: This is the integer part, like the 3 whole slices of pie you ate.
- Fraction: This represents the remaining part that isn’t a whole number, like the ¼ slice you wanted from the fourth piece.
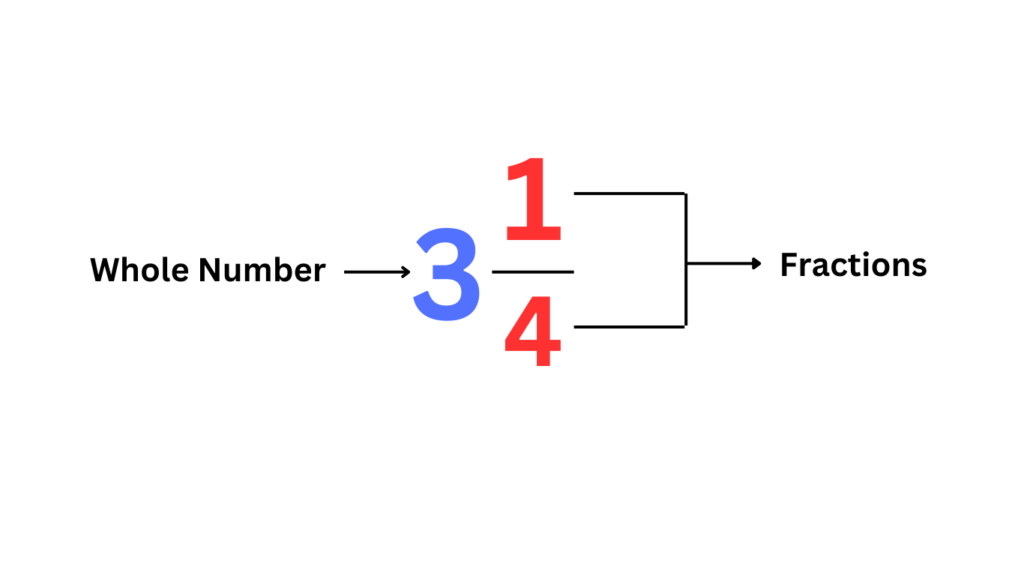
So, whenever you see a number like 2½ or 4 ¾, you’re looking at a mixed fraction.
Now, mixed fractions have a close cousin called improper fractions. These are fractions where the numerator (the top number) is bigger than the denominator (the bottom number). For example, 4/3 is an improper fraction because 4 is larger than 3. We can convert mixed fractions to improper fractions, and vice versa, which will come in the later part of the article.
Addition of Mixed Fractions
Let’s get started with the exciting world of adding mixed fractions. But first, things are a bit smoother if the mixed fractions have the same denominator, just like having pie slices of the same size.
Here’s how to add mixed fractions with the same denominator:
- Add the whole numbers: Focus on the whole number parts of the fractions and simply add them together. Let’s say you have 1 and 1/4 apples and you need to add 2 and 1/4 more apples. Here, first, we will add the whole numbers: 1 + 2 = 3
- Add the fractions: Now, add the fractional parts just like you would add any fractions. So, in the above example, after getting the result of whole numbers, we will add the fraction: 1/4 + 1/4 = 1/2
- Combine the results: Write down the sum of the whole numbers as the whole number part of the answer, and the sum of the fractions as the fractional part. So, if we add 1 and 1/4 apples and 2 and 1/4 more apples then we will get 3 and 1/2 apples.
But what if they have different denominators, like pie slices of different sizes? Don’t worry, we can still add them. We just need a little trick called finding the least common denominator (LCD).
The LCD is the smallest number that both denominators (the bottom numbers) can divide into evenly. Once we have the LCD, we can convert our fractions to have that denominator and then add them as usual.
For example, let’s add 2¼ + 1½. Here’s the breakdown:
- Whole numbers: 2 + 1 = 3
- Since we have different denominators, we first make the denominators the same, by using the trick of finding the least common denominator: (1/2) × (2/2) = 2/4
- Add Fractions: 1/4+ 2/4 = 3/4
- Combine results: So, 2¼ + 1½ = 3 ¾
Subtraction of Mixed Fractions
Subtracting mixed fractions follows a similar approach to addition. Again, things are easier if the fractions have the same denominator. Here’s the process:
- Subtract the whole numbers: Just like addition, focus on the whole numbers first and subtract them. Suppose you have 3 and 3/4 cookies, and you eat 1 and 1/4 cookies. Here first you subtract the whole numbers: 3 – 1 = 2.
- Subtract the fractions: Now, subtract the fractional parts just like you would subtract any fractions. So, in the above example, after getting the result of whole numbers, we will subtract the fraction: 3/4 – 1/4 = 1/2
- Combine the results: Write down the difference of the whole numbers as the whole number part of the answer, and the difference of the fractions as the fractional part. So, if we subtract 1 and 1/4 cookies from 3 and 3/4 cookies then we will get 2 and 1/2 apples.
Similarly, if there are different denominators, we will just follow as we did earlier in the addition, i.e. make the denominators the same by using the trick of Least Common Denominator and solve our subtraction problem.
For example, let’s subtract 4½ – 1¼. Here’s the breakdown:
- Whole numbers: 4 – 1 = 2
- Since we have different denominators, we first make the denominators the same, by using the trick of finding the least common denominator: (1/2) × (2/2) = 2/4
- Subtract Fractions: 2/4- 1/4 = 1/4
- Combine results: So, 4½ – 1¼ = 2 ¼
Multiplication of Mixed Fractions
Multiplication with mixed fractions might seem like a challenge, but it’s actually quite straightforward. We can break it down into multiplying by a whole number. Imagine you have a recipe that calls for 1 ½ cups of flour for a single batch of cookies. But what if you want to bake double the amount? Here’s where multiplying mixed fractions comes in handy!
In essence, multiplying a mixed fraction by a whole number is like multiplying each part (the whole number and the fraction) by the whole number separately. Here’s how it works:
- Multiply the whole number part: Take the whole number part of the mixed fraction and multiply it by the whole number you’re multiplying by.
- Multiply the fractional part: Multiply the fractional part of the mixed fraction by the whole number you’re multiplying by.
- Combine the results: Add the product you got from the whole number part (step 1) and the product you got from the fractional part (step 2). This will be your final answer.
Let’s use the cookie recipe example. We need to multiply 1 ½ by 2 (because we want to double the recipe). Here’s the breakdown:
- Whole number part: 1 x 2 = 2
- Fractional part: ½ x 2 = 1 (remember, ½ multiplied by 2 is the same as getting two ½ slices)
Now, add the product from the whole number part (2) and the product from the fractional part (1): 2 + 1 = 3.
Therefore, to make double the recipe, you’ll need 3 cups of flour (which can be written as the mixed fraction 3 0/2, but since there’s no fractional part, it’s simply 3).
Division of Mixed Fractions
Division might seem like the trickiest operation with mixed fractions, but don’t be intimidated. Division can be understood as splitting something into equal groups.
Here’s how to tackle dividing a mixed fraction by a whole number:
- Think in terms of wholes: Imagine the mixed fraction represents a whole unit (like a cake).
- Split it into equal groups: Divide the whole number part of the mixed fraction by the whole number you’re dividing by. This tells you how many equal groups you have.
For example, let’s divide 4 ½ by 2. Think of 4 ½ as a whole cake. If we cut it into 2 equal groups, what size would each piece be?
- Whole number part: 4 / 2 = 2
So, each person would get a piece that’s the size of a whole number 2 (or we can say 2 wholes). There wouldn’t be any leftover fractional parts because we’re dividing by a whole number.
Dividing mixed fractions by fractions is a bit more complex, but there’s a neat trick! We can actually flip the fraction we’re dividing by (the divisor) and multiply instead. This “flipping” is the same as taking the reciprocal of the divisor.
For example, instead of dividing 3 ½ by ½, we can flip ½ to its reciprocal (which is 2/1) and multiply: 3 ½ x 2/1. We have explored this concept in our previous article, you can check it out: Mastering How to Multiply Fractions: Ignite Your Fraction Mastery and Empower Your Math Skills with Confidence (2024)
Converting Between Mixed Fractions and Improper Fractions
Remember how we mentioned improper fractions earlier? These are fractions where the numerator (top number) is bigger than the denominator (bottom number). Well, mixed fractions and improper fractions can be converted into each other.
Converting a Mixed Fraction to an Improper Fraction
Imagine you have a pizza cut into 8 slices. You’ve eaten 2 whole slices and have 3 slices left over. This can be represented as the mixed fraction 2 ¾. But we can convert this to an improper fraction:
- Multiply the whole number part by the denominator of the fraction: In this case, 2 x 4 (denominator of ¾) = 8.
- Add the product to the numerator of the fraction: 8 (from step 1) + 3 (the numerator of ¾) = 11.
- The new numerator becomes the numerator of the improper fraction, and the denominator stays the same: Our improper fraction becomes 11/4.
So, 2 ¾ is equivalent to 11/4. Now, using this technique of conversion, we can solve the addition, subtraction, multiplication, and division problem of mixed fractions. Simply convert the mixed fraction into improper fractions and use the method of fractions to solve these problems.
Converting an Improper Fraction to a Mixed Fraction
We’ve already explored how to convert mixed fractions to improper fractions. But did you know you can also go the other way around? This conversion can be helpful when you encounter a recipe written in improper fractions (like needing 11/4 cups of flour) and want to visualize it as whole numbers and fractional parts.
Here’s the basic idea behind converting an improper fraction to a mixed fraction:
- Imagine the numerator (top number) of the improper fraction represents a bunch of objects, like whole cookies.
- The denominator (bottom number) tells you the size or value of each object.
Our goal is to group these objects (represented by the numerator) into wholes (the whole number part of the mixed fraction) with some leftover parts (the fractional part of the mixed fraction).
The conversion process involves dividing the numerator by the denominator. Here’s a step-by-step breakdown:
- Divide the numerator by the denominator: Perform a division calculation with the numerator as the dividend and the denominator as the divisor.
- The quotient (the result of the division) becomes the whole number part of the mixed fraction: This tells you how many whole groups you were able to create from the numerator.
- The remainder (leftover after the division) becomes the numerator of the fractional part of the mixed fraction: This represents the leftover objects that couldn’t be grouped into wholes and remain as a fraction.
- The denominator of the mixed fraction stays the same as the denominator of the original improper fraction.
Applications of Mixed Fractions in Everyday Life
Mixed fractions aren’t just mathematical concepts confined to textbooks. They play a surprisingly important role in our everyday lives. Here are some real-world examples where they come in handy:
- Recipe Magic: Baking a cake, mixing a batch of cookies, or preparing a delicious salad dressing – all these culinary creations often involve ingredients measured in mixed fractions. Imagine a recipe calling for 2 ¾ cups of flour or 1 ½ teaspoons of baking powder. Understanding mixed fractions ensures you have the right proportions for a perfect outcome!
- Carpentry Calculations: Whether you’re building a bookshelf or crafting a DIY project, they are essential for accurate measurements. You might need to cut a piece of wood that’s 3 ½ feet long or drill holes that are spaced ½ inch apart. Precise measurements using mixed fractions guarantee a well-constructed project.
- Timekeeping Twists: While we often use decimals for time, they can be helpful when dealing with elapsed time or remaining durations. For example, a movie that runs for 2 hours and 15 minutes can be written as 2 ¼ hours. Understanding mixed fractions helps you calculate how long a task will take or how much time remains until an event.
- Sharing and Dividing: Let’s say you have a pizza cut into 8 slices and want to share it equally among 3 friends. Each person would receive 2 ¾ slices (8 slices divided by 3 people). Mixed fractions come in handy when splitting things like fabric, paint, or rope into equal portions.
Beyond these examples, they have applications in various fields like textile design, graphic arts, and even sports statistics. The ability to work with mixed fractions equips you with valuable problem-solving skills applicable to various aspects of life.
Conclusion
Congratulations! You’ve reached the end of this comprehensive guide on mixed fractions. We’ve explored addition, subtraction, multiplication, division, and conversions, equipping you with the knowledge and tools to tackle them with confidence.
Remember, practice is key. There are many online resources and worksheets available to help you hone your mixed fraction skills. The more you practice, the more comfortable and confident you’ll become.
Understanding mixed fractions is not just about performing calculations; it’s about developing a deeper understanding of parts and wholes. This skill translates into clear thinking, problem-solving abilities, and a newfound appreciation for the precision and beauty of mathematics.
So, the next time you encounter them in a recipe, a DIY project, or even while calculating elapsed time, remember – you have the knowledge and tools to conquer it.
Frequently Asked Questions (FAQs)
Why are mixed fractions important?
Mixed fractions are crucial for everyday tasks like cooking, crafting, and time management. They also serve as a foundation for more complex mathematical concepts.
What’s the difference between mixed fractions and improper fractions?
Mixed fractions combine a whole number and a proper fraction, while improper fractions have a numerator greater than the denominator.
Can you convert between mixed fractions and improper fractions?
Yes, you can convert between mixed fractions and improper fractions. To convert to an improper fraction, multiply the whole number by the denominator and add the numerator. To convert back, divide the numerator by the denominator to get the whole number and use the remainder as the numerator for the fractional part.