Table of Contents
Introduction
Welcome to the enchanting realm of multiplication, where numbers come alive in a magical dance of patterns and possibilities. In this article, we’ll embark on a whimsical journey beyond the mundane times tables, exploring the mysteries of multiplication magic. Get ready to uncover the secrets, decode the patterns, and witness the beauty that lies within the world of multiplication.
The Foundation: Understanding Multiplication
Before we delve into the magic, let’s revisit the basics of multiplication. At its essence, multiplication is a mathematical operation that combines groups of numbers to find the total. Instead of adding a number repeatedly, multiplication provides a shortcut to determine the outcome swiftly.
The Star of the Show: The Multiplication Symbol (×)
The multiplication symbol (×) is the star of our magical production. Just like a wand in the hands of a wizard, the symbol transforms ordinary numbers into extraordinary results. It’s a signal for numbers to come together and create something new.
Magic Trick #1: The Commutative Property
One of the first magic tricks in the world of multiplication is the commutative property. It’s like a ballet where the order of the dancers doesn’t matter; the performance remains the same. In multiplication, changing the order of the numbers doesn’t change the result.
Example:
3 × 5 = 5 × 3
Whether you have 3 groups of 5 or 5 groups of 3, the magic product is always 15. It’s a commutative ballet where the numbers pirouette without altering the outcome.
Magic Trick #2: The Associative Spectacle
In the associative property, numbers perform acrobatics by regrouping themselves. It’s a spectacular display where the grouping of numbers changes, but the outcome remains constant. It’s like a circus act where the performers switch partners seamlessly.
Example:
(2 × 3) × 4 = 2 × (3 × 4)
Whether you group 2 with 3 first or 3 with 4 first, the result is always 24. It’s an associative spectacle where numbers dazzle in their ability to regroup and maintain the magic.
Magic Trick #3: The Distributive Illusion
The distributive property is a magical illusion where a number distributes itself among the members of a group. It’s like a magician’s cloak that can cover multiple objects at once. A number outside the parentheses distributes itself to each term inside.
Example:
2 × (5 + 3) = (2 × 5) + (2 × 3)
The magic here is that whether you multiply 2 by the sum of 5 and 3 or individually by 5 and 3 first, the result is 16. It’s a distributive illusion.
Magic Trick #4: The Zero Wizardry
Zero has a unique role in the world of multiplication. When any number is multiplied by zero, the result is always zero. It’s like a sorcerer’s spell where zero has the power to make any number vanish.
Example:
7 × 0 = 0
No matter how large or small the number, when multiplied by zero, it succumbs to the magic, and the result is zero. It’s zero magic that adds a touch of mystery to the multiplying stage.
Multiplication Mastery: Beyond the Times Tables
The Joy of Patterns
The times tables are the gateway to multiplication mastery, but the real magic lies in understanding the patterns within them. Each set of times tables reveals a symphony of numerical relationships waiting to be explored.
Example:
Consider the 9 times table:
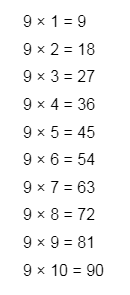
Notice the pattern in the unit place: 9, 8, 7, 6, 5, 4, 3, 2, 1, and 0. It’s a descending sequence, a magical pattern within the timestable symphony. Similarly, in the tens place, the number is in an ascending sequence: 1, 2, 3, 4, 5, 6, 7, 8, and 9. So, remember whenever you are writing the times table of nine you can just follow this pattern.
The Power of Multiples
Multiples are like the footprints of multiplication magic. Understanding multiples helps uncover the relationships between numbers and reveals the intricate dance of factors.
Example:
Consider the multiples of 4:
4, 8, 12, 16, 20, …
Each number is a magical multiple of 4, showcasing the power of multiplication in creating a rhythmic sequence.
Prime Numbers: The Unicorns of Multiplying
Prime numbers are the unicorns of the multiplication kingdom. They are the numbers that can only be multiplied by 1 and themselves without any other factors. It’s a unique magic that sets them apart in the numerical landscape.
Example:
2, 3, 5, 7, 11, …
Each prime number stands alone in its magical identity, refusing to be divided by any other number but 1 and itself.
Multiplication in Everyday Magic
Cooking
In the kitchen, multiplication transforms recipes into culinary adventures. It helps in adjusting ingredient quantities and scaling recipes up or down. It is like a magical touch that is required in cooking.
Example:
If a recipe calls for 2 cups of flour and you want to double it:
2 cups × 2 = 4 cups
When you are multiplying it is like magic that ensures a delightful culinary outcome.
Time Travel
When planning schedules and managing time, multiplication is the time traveler’s tool. It is necessary when calculating durations, estimating arrival times, and organizing daily activities.
Example
If your commute takes 30 minutes, and you need to make the journey twice a day:
30 minutes × 2 = 60 minutes
See, the magic of multiplying ensures you stay on a time-travel schedule.
Conclusion
As we wrap up our journey beyond the times tables, it’s evident that multiplication is not just a mathematical operation; it’s a magical spectacle. From the commutative and associative properties to distributive illusions and zero wizardries, it weaves its magic across numbers, creating patterns and relationships that captivate the mathematical imagination.
So, the next time you encounter a problem to multiply, don’t just see it as a task. Dive into the magical world of multiplication with curiosity and enthusiasm, and unravel the mysteries that make it a truly enchanting experience.
Frequently Asked Questions (FAQs)
Why is understanding the commutative property important?
Understanding the commutative property is crucial because it simplifies calculations. Whether you’re dealing with small numbers or large ones, knowing that the order of operations doesn’t change the result can save time and effort.
How does the distributive property make multiplication easier to understand?
The distributive property simplifies multiplication by breaking it into smaller, more manageable steps. Distributing a number across the terms inside parentheses allows a clearer understanding of how operations interact with addition.
Why is zero considered a magical element during multiplying?
Zero’s magic during multiplying lies in its ability to make any number it touches disappear. Understanding this concept is essential because it helps us grasp the unique role zero plays in determining the outcome of multiplication with any other number.