Perpendicular Lines – Unveiling the Secrets of Perfect Right Angles (2024)

Introduction

Ever built a bookshelf, only to find the shelves leaning precariously, creating a wobbly mess? Or maybe you’ve attempted to hang a picture frame, but it stubbornly refuses to sit straight. These frustrating situations highlight the importance of perpendicular lines – the secret weapon for creating perfect right angles and ensuring stability in our everyday world.

So, ditch the wonky shelves and lopsided pictures. Today, we’ll embark on a journey into the fascinating realm of perpendicular lines. We’ll unveil their mysteries, explore their real-world applications, and empower you to become a pro at identifying these geometric gems.

What are Perpendicular Lines?

To start with the basics, perpendicular lines are two lines that intersect at a right angle (90 degrees). In geometry, this special relationship is often denoted by the symbol ⊥. When two lines are perpendicular, they form four right angles at their point of intersection. This property makes them incredibly useful in various mathematical and practical applications.

For example, think of the corners of a square or rectangle. Each corner forms a right angle, and the sides that meet at these corners are perpendicular to each other. This simple yet powerful concept forms the foundation of much of our understanding of shapes, structures, and spaces.

To solidify this concept, take a look at the image below:

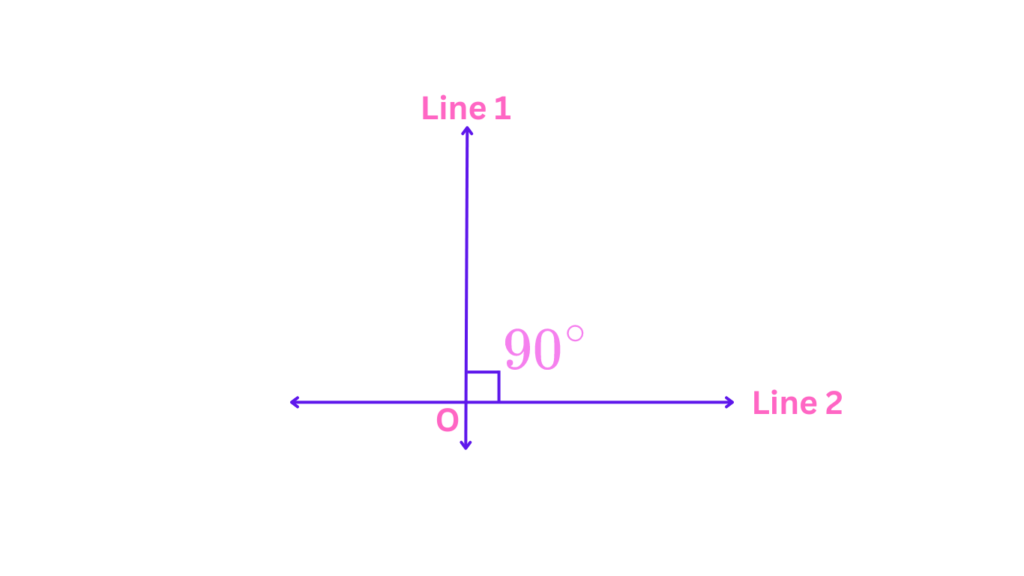
See how Line 1 and Line 2 meet at a precise 90-degree angle? This is the defining characteristic of perpendicular lines. They create a perfect right angle, forming the foundation for countless geometric shapes and structures.

Properties of Perpendicular Lines

Understanding the properties of perpendicular lines helps us appreciate their role in both theoretical and applied mathematics. So, now that you’ve grasped the basic concept, let’s delve deeper into its properties:

• Right Angles (90 Degrees): The defining feature of perpendicular lines is that they intersect to form right angles. This means that each of the four angles created at the intersection point is exactly 90 degrees. This property is fundamental in geometry and is used to define shapes like squares and rectangles.
• Relationship Between Perpendicular Lines and Axes in Coordinate Geometry: In the coordinate plane, these lines have slopes that are negative reciprocals of each other. For instance, if one line has a slope of ‘m’, the line perpendicular to it will have a slope of -1/m​. This relationship is crucial when working with linear equations and graphing lines in algebra.
• Congruent Opposite Sides: While not always the case, in some specific situations like perfect squares, the opposite sides of these lines might also be equal in length. However, this additional property is not a requirement for all perpendicular lines. The key takeaway is the perfect 90-degree angle at the point of intersection.

Real-World Applications of Perpendicular Lines

The beauty of geometry lies in its ability to translate into the real world. Perpendicular lines are no exception. These lines are not just theoretical constructs; they have numerous practical applications in various fields Here are some surprising places where you might encounter them:

• Architecture and Construction: In architecture, perpendicular lines ensure structural stability and aesthetic appeal. Building designs, floor plans, and structural frameworks rely heavily on perpendicular intersections to maintain right angles. This is crucial for creating balanced, safe, and functional buildings. Imagine a house – the walls meet at right angles, creating a stable structure that can withstand everyday wear and tear.
• Urban Planning and Road Design: Urban planners use these lines to design efficient road systems. Intersecting roads at right angles helps in managing traffic flow and ensuring safety at intersections. The grid layout commonly seen in cities relies on perpendicular lines to organize streets and avenues systematically.
• Art and Design: The world of art and design heavily relies on geometric shapes, and perpendicular lines are a fundamental building block. They form the basis of squares, rectangles, and other geometric shapes used in paintings, sculptures, and architectural designs. The perfect symmetry and balance created by these lines add a sense of order and beauty to our visual surroundings.
• Furniture Design: Whether it’s your sturdy dining table or your comfortable armchair, these lines play a crucial role in furniture design. They ensure tables don’t wobble, chairs stand tall, and bookshelves provide a stable platform for your favorite reads.
• Navigation: Believe it or not, understanding these lines can help you navigate. Understanding these lines helps with using a compass, where cardinal directions (north, south, east, west) form perfect right angles for navigation.
• Video Games: These lines are also used in creating stable structures, properly aligned objects and realistic 3D environments within video games.
• Photography: These lines are used as a compositional tool to create a sense of balance and stability in photographs.

Identifying Perpendicular Lines

Feeling ready to conquer the world of perpendicular lines? Here’s a simple guide to help you identify them in the wild:

• The All-Seeing Eye: The most accurate way to identify these lines is by measuring the angle at the point of intersection. A standard protractor, a tool designed to measure angles, can be your trusty companion in this quest. If the angle measures exactly 90 degrees, congratulations, you’ve found a pair of perpendicular lines.

• The “L” Shape Test: Don’t have a protractor handy? No worries! The good old “L” shape test can still come to your rescue. Imagine placing a perfect “L” cutout (like a corner of a square) on the lines you’re investigating. If the lines perfectly match the two arms of the “L,” forming a seamless right angle, then you’ve found your perpendicular lines.

• The Square Spotter: Keep an eye out for naturally occurring squares in your surroundings. Remember, all squares are made with four perpendicular lines. So, if you find a square window pane, a well-tiled floor, or even a perfectly aligned book on a shelf, you’ve stumbled upon a real-life example of perpendicular lines in action.

How to Draw Perpendicular Lines

Drawing perpendicular lines is a fundamental skill in geometry, art, and construction. Here’s how you can do it:

• Using a Protractor and Ruler:

1. Draw the Base-Line: Start by drawing a straight line using a ruler. This will be your base-line.
2. Align the Protractor: Place the midpoint of the protractor on a point along the base-line where you want the perpendicular line to intersect.
3. Mark the Right Angle: Using the protractor, mark a point at 90 degrees from the base-line.
4. Draw the Perpendicular Line: Using the ruler, draw a straight line through the point marked at 90 degrees, ensuring it crosses the base-line. This new line is perpendicular to the base-line.

• Using a Compass:

1. Draw the Base-Line: Begin with a straight base-line.
2. Choose the Intersection Point: Select a point on the base-line where you want the perpendicular line to intersect.
3. Set the Compass Width: Open the compass to a comfortable width that is less than the length of the base line.
4. Draw Arcs: Place the compass point on the chosen intersection point and draw an arc above and below the base-line.
5. Intersect the Arcs: Without changing the compass width, place the compass point on the intersections of the arcs with the base-line and draw two more arcs that intersect each other above and below the base-line.
6. Draw the Perpendicular Line: Draw a straight line through the points where the arcs intersect above and below the base-line. This line is perpendicular to the base-line.

Common Misconceptions

Clearing up misconceptions helps solidify our understanding of perpendicular lines.

• Difference Between Perpendicular Lines and Intersecting Lines: While all perpendicular lines intersect, not all intersecting lines are perpendicular. Intersecting lines cross at any angle, while perpendicular lines specifically intersect at a right angle (90 degrees).
• Clarifying the Concept of Parallel Lines vs. Perpendicular Lines: Parallel lines never intersect and remain equidistant from each other, while perpendicular lines intersect at right angles. Understanding this distinction is crucial in geometry and various applications.

Conclusion

Perpendicular lines are a fundamental concept in geometry, playing a crucial role in both theoretical and practical applications. From their defining right angles to their numerous real-world uses, understanding these lines enriches our appreciation of the structures and designs around us. Next time you look at a street sign, a piece of paper, or a building, take a moment to appreciate the magic of these lines. Keep exploring the geometric world around you, and you’ll find that these lines are indeed fascinating and essential.

Frequently Asked Questions (FAQs)

What are Perpendicular Lines?

Perpendicular lines are two lines that intersect at a right angle (90 degrees). This special relationship is fundamental in geometry and various practical applications.

How Are Perpendicular Lines Different from Parallel Lines?

Perpendicular lines intersect at right angles, while parallel lines never intersect and remain equidistant from each other. This distinction is crucial in understanding geometric relationships.

Can Perpendicular Lines Exist in Three Dimensions?

Yes, perpendicular lines can exist in three-dimensional space. In three dimensions, two lines are perpendicular if they intersect at a right angle and lie in the same plane.

How Do You Identify Perpendicular Lines on a Graph?

On a graph, perpendicular lines have slopes that are negative reciprocals of each other. If you know the slope of one line, the slope of these lines can be found by taking the negative reciprocal.