Prime and Composite Numbers: Unveiling the Magic of Mathematical Marvels (2024)

Have you ever wondered if there’s a secret code hidden within numbers? Well, the world of prime and composite numbers holds a fascinating key to understanding how numbers can be broken down and built up.

In mathematics, prime and composite numbers stand as pillars of numerical distinction, defining the very essence of divisibility. So, in this article, we’ll embark on a journey to explore these special categories of numbers, unveil their properties, and discover how they play a vital role in mathematics and beyond. Buckle up, because we’re about to dive into the thrilling realm of prime and composite numbers.

What are Prime and Composite Numbers?

At the heart of prime and composite numbers lies the concept of divisibility. Simply put, divisibility refers to the ability of one number (the divisor) to divide evenly into another number (the dividend) with no remainder. Now, let’s meet the stars of the show, prime and composite numbers:

Prime Numbers

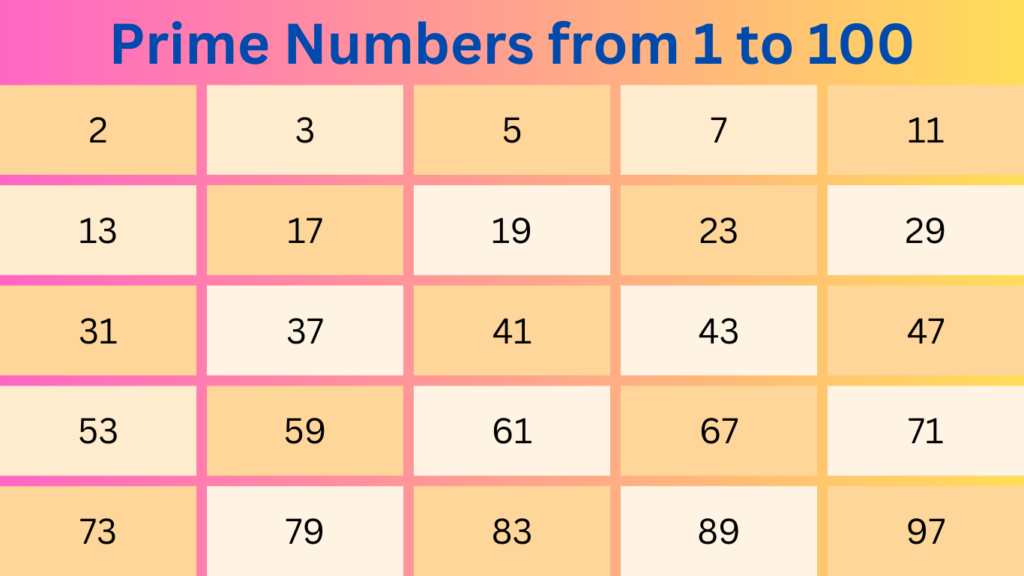
Prime numbers are the superstars. Prime numbers are whole numbers greater than 1 that have exactly two distinct positive divisors: 1 and themselves. Imagine a prime number as a solitary dancer, perfectly in sync with itself and the music (the concept of 1). No other whole number can divide it cleanly without leaving a leftover “remainder” partner. Some examples of prime numbers include 2, 3, 5, 7, and 11.

Composite Numbers

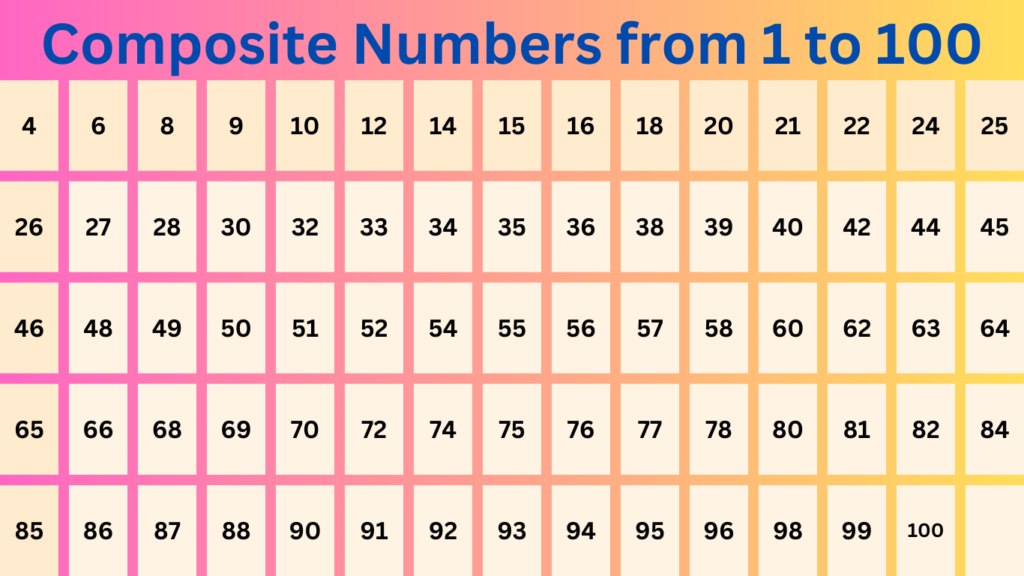
Composite numbers are the party animals. Composite numbers are whole numbers greater than 1 that have more than two distinct positive divisors. Think of them as a group of dancers, where you can easily pair them up with different partners (divisors) for a lively performance. For instance, 6 can be divided by 1, 2, 3, and 6. Other composite numbers include 4, 8, 9, and 10.

The key difference between prime and composite numbers boils down to divisibility. Prime numbers are like loners, content with just their own company (1) and themselves, while composite numbers are social butterflies with multiple divisibility partners.

Identifying Prime and Composite Numbers

So, how do we tell these numbers apart? Here are some detective skills to hone your prime and composite number identification prowess:

• Divisibility Rules for Prime Numbers (Small Ones): For smaller prime numbers, we have handy divisibility rules. For example, any even number (divisible by 2) cannot be prime (except for 2 itself) because it has at least two divisors (1 and 2). Similarly, a number ending in 5 or 0 can only be prime if it’s 2 or 5, respectively.
• Primality Tests for Larger Numbers: When dealing with larger numbers, things get a bit trickier. One method is called trial division. Here, you systematically check if the number is divisible by all smaller prime numbers (up to the square root of the number). If none of them are divided evenly, then the number is prime. This can be a time-consuming process for very large numbers.
• Composite Number Identification: Identifying composite numbers is simpler. If you find more than two distinct positive divisors (excluding 1 and itself) for a number, then it’s a composite number. For instance, the number 12 has the divisors 1, 2, 3, 4, 6, and 12, revealing its composite nature.

Properties of Prime Numbers: The Power of Uniqueness

Prime numbers aren’t just about being solitary; they possess some unique properties that make them special:

• Unique Factorization: Every composite number can be expressed as a product of prime numbers uniquely, like building blocks coming together to form a larger structure. This is known as the Fundamental Theorem of Arithmetic. Imagine the number 15; its prime factorization is 3 x 5. No other combination of prime numbers can create 15.
• Infinite Primes: Here’s a mind-boggling fact. Euclid, a mathematician from ancient Greece, proved that there are infinitely many prime numbers. This means the list of primes goes on forever, like an endless starry sky.

Sieve of Eratosthenes: A Flourishing Tool for Prime Number Discovery

The Sieve of Eratosthenes, a brilliant invention by the ancient Greek mathematician Eratosthenes, is an efficient and elegant method for identifying prime numbers within a specific range. Imagine a bountiful harvest, where you need to separate the prime grains (prime numbers) from the rest. The Sieve of Eratosthenes acts like a sophisticated sieve, systematically filtering out composite numbers to reveal the primes.

Unveiling Primes with the Sieve

The method is based on a simple yet powerful observation: if a number is composite (divisible by a prime number greater than 1), then all its multiples will also be composite. Here’s how the sieve works:

1. Create a List: Write down all the positive integers starting from 2 (the smallest prime number) up to your desired limit.
2. Prime Power Play: Take the first uncrossed number (let’s say 2, the first prime). Cross out all the multiples of 2 from the list, starting from 4 (2 x 2). Why? Because any number divisible by 2 is guaranteed to be composite (except for 2 itself).
3. Sieving the Multiples: Move on to the next uncrossed number (the next prime number after 2). Let’s say it’s 3. Now, systematically cross out all the multiples of 3 from the list, starting from 6 (3 x 2) and continuing at regular intervals of 3 (9, 12, 15, and so on). Again, these multiples are guaranteed to be composite.
4. Repeat and Refine: Continue this process. Take the next uncrossed prime number and eliminate all its multiples from the list. The key is to only consider uncrossed prime numbers for sieving, as their multiples have already been taken care of in previous steps.
5. Prime Harvest: Once you’ve reached the square root of your upper limit (because no prime number can have another prime factor greater than its square root), all the remaining uncrossed numbers are prime.

Finding Primes with the Sieve

Let’s use the Sieve of Eratosthenes to find prime numbers up to 20:

1. List Creation: We write down the numbers 2 to 20.
2. Sieving with 2: We cross out 4, 6, 8, 10, 12, 14, 16, 18, and 20 (multiples of 2).
3. Sieving with 3: We cross out 6, 9, 12, 15, and 18 (multiples of 3 that weren’t previously crossed out by 2).
4. Sieving with 5 (no multiples between 3 and 5 in our range): We move on to 5 and cross out 10 (the only multiple of 5 within our range).
5. Prime Harvest: Since we’ve reached the square root of 20 (which is about 4.5), all the remaining uncrossed numbers (2, 3, 5, 7, 11, 13, 17, and 19) are prime!

The Sieve of Eratosthenes, with its efficient elimination process, is a valuable tool for uncovering prime numbers within a designated range. This method has stood the test of time, remaining a fundamental technique for prime number discovery.

The Importance of Prime and Composite Numbers

Prime and composite numbers aren’t just mathematical curiosities; they play a vital role in various fields:

• Number Theory: Prime numbers are the building blocks of number theory, a branch of mathematics that explores the properties of numbers. Understanding prime factorization helps us solve problems related to divisibility, greatest common divisors, and least common multiples.
• Cryptography: In today’s digital world, prime numbers are crucial for secure communication. Encryption techniques like RSA rely on the difficulty of factoring large prime numbers, keeping your online messages safe from prying eyes.
• Real-World Applications: Even in everyday life, prime and composite numbers can be surprisingly useful. For example, ensuring equal distribution of cookies among friends requires checking for a prime number of cookies (so there are no leftover halves). Similarly, understanding divisibility by 2 (even vs. odd) helps predict if the sum of two numbers will be even or odd.

Fun Facts and Activities

The world of prime numbers is full of fascinating facts and activities to keep your mind buzzing:

• The Biggest Prime Number (as of Today): As of 2023, the largest known prime number is a monstrous number with over 24 million digits. It’s mind-blowing to think there are even bigger primes out there waiting to be discovered.
• Prime Number Challenges: Test your prime-spotting skills with online quizzes and puzzles that challenge you to identify prime numbers within a specific range or based on certain criteria.
• Number Sieve of Eratosthenes: This is a fun activity to discover prime numbers up to a certain limit. Imagine a sieve – a tool for separating things. Here, you systematically eliminate composite numbers from a list of consecutive whole numbers, leaving behind the primes like grains of truth.

Conclusion

We’ve embarked on a thrilling journey through the realm of prime and composite numbers. We’ve learned to identify them, explored their unique properties, and discovered their significance in mathematics and the real world. Remember, prime numbers may be loners, but they hold immense power in the grand scheme of numbers.

As you delve deeper into mathematics, you’ll encounter prime numbers resurfacing in fascinating areas like:

• Perfect numbers: These are special numbers equal to the sum of their proper divisors (divisors excluding the number itself). Only a handful of perfect numbers are known, and mathematicians are still searching for more!
• Goldbach’s conjecture: This unsolved problem in number theory proposes that every even number greater than 2 can be expressed as the sum of two prime numbers. While mathematicians have verified this conjecture for incredibly large numbers, a definitive proof remains elusive.

The world of prime and composite numbers is a gateway to a universe of mathematical exploration. So, keep your curiosity alive, keep practicing your divisibility skills, and who knows, you might even be the one to crack the next big prime number mystery.

Frequently Asked Questions (FAQs)

What are prime and composite numbers?

Prime numbers are whole numbers greater than 1 with exactly two distinct positive divisors, while composite numbers have more than two distinct positive divisors.

How can I identify prime and composite numbers?

Prime numbers have only two divisors, 1 and themselves, whereas composite numbers have multiple divisors beyond 1 and themselves.

What are some real-world applications of prime and composite numbers?

Prime and composite numbers find applications in cryptography, number theory, and various everyday scenarios like distribution problems and determining the parity of sums.