Introduction
Have you ever wondered how we can break down large numbers into their basic building blocks? Welcome to the fascinating world of prime factorization. This essential mathematical tool allows us to deconstruct any number into a product of prime numbers. Whether you’re a student, a math enthusiast, or someone who simply loves learning, understanding prime factorization can open up a world of numerical magic. In this comprehensive guide, we’ll walk you through everything you need to know about prime factorization, including its importance, methods, applications, and some handy tips and tricks.
Understanding Prime Factorization
Definition
Prime factorization is the process of expressing a number as the product of its prime factors. For example, the prime factorization of 18 is 2×3^2. Similarly, prime factors are the prime numbers that multiply together to give the original number. This concept is fundamental in various areas of mathematics, including algebra, number theory, and even in practical applications like cryptography.
Importance
Why is it so important? It’s because prime numbers are the building blocks of all natural numbers. Understanding how to break down a number into its prime components can help simplify complex mathematical problems, find common denominators, and even secure digital information. In essence, it is a powerful tool that enhances our mathematical toolbox.
What are Prime Numbers?
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This means a prime number cannot be formed by multiplying two smaller natural numbers.
Examples of Prime Numbers
Some of the first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29. Notably, 2 is the only even prime number, as all other even numbers can be divided by 2.
Prime vs. Composite Numbers
In contrast to prime numbers, composite numbers have more than two positive divisors. For instance, the number 6 is composite because it can be divided evenly by 1, 2, 3, and 6. Understanding the difference between prime and composite numbers is crucial for mastering prime factorization.
The Process of Prime Factorization
Let’s dive into the step-by-step process of prime factorization with some clear examples:
Step 1: Identify if the number is prime or composite. If the number is prime, its prime factorization is the number itself.
Step 2: Find the smallest prime number that divides the composite number. This could be 2, 3, 5, or any other prime number.
Step 3: Divide the number by the prime number. Keep dividing until the quotient is no longer divisible by that prime.
Step 4: Repeat the process with the quotient until all factors are prime. Continue this process until all remaining factors are prime numbers.
Example 1: Prime factorization of 60.
- 60 is not a prime number (it’s composite).
- The smallest prime number that divides 60 is 2.
- 60÷2=30.
- 30÷2=15.
- The smallest prime number that divides 15 is 3.
- 15÷3=5.
- 5 is a prime number.
So, the prime factorization of 60 is 2×2×3×5 or 2^2×3×5.
Example 2: Prime factorization of 84.
- 84 is not a prime number (it’s composite).
- The smallest prime number that divides 84 is 2.
- 84÷2=42.
- 42÷2=21.
- The smallest prime number that divides 21 is 3.
- 21÷3=7.
- 7 is a prime number.
So, the prime factorization of 84 is 2×2×3×7 or 2^2×3×7.
Prime Factorization Methods
There are several methods to perform prime factorization. Here, we’ll explore two common techniques: factor trees and the division method.
Factor Trees
A factor tree is a graphical representation that helps break down a number into its prime factors. Start by writing the composite number at the top, then draw branches down to its factors. Continue breaking down each composite factor until all branches end in prime numbers.
Example: Here is an example of the number 72.
Step 1: We start with 72 at the top of the tree.
Step 2: Since 72 is even, see if it’s divisible by 2. It is, so divide 72 by 2 and write 2 on the left branch and 36 on the right branch.
Step 3: Continue dividing the right branch by 2 as long as it’s divisible. We can keep dividing 36 by 2 until we reach 2. So we have 2 on the left for each division and update the right branch accordingly (36, 18, 9).
Step 4: Now focus on the number 9 on the right branch. Since 9 is odd, we move to the next prime number, 3. We see 9 is divisible by 3, so write 3 on the left branch and 3 on the right branch.
Step 5: Finally, 3 is a prime number, so we can’t divide it further. We reach the end of the factorization process.
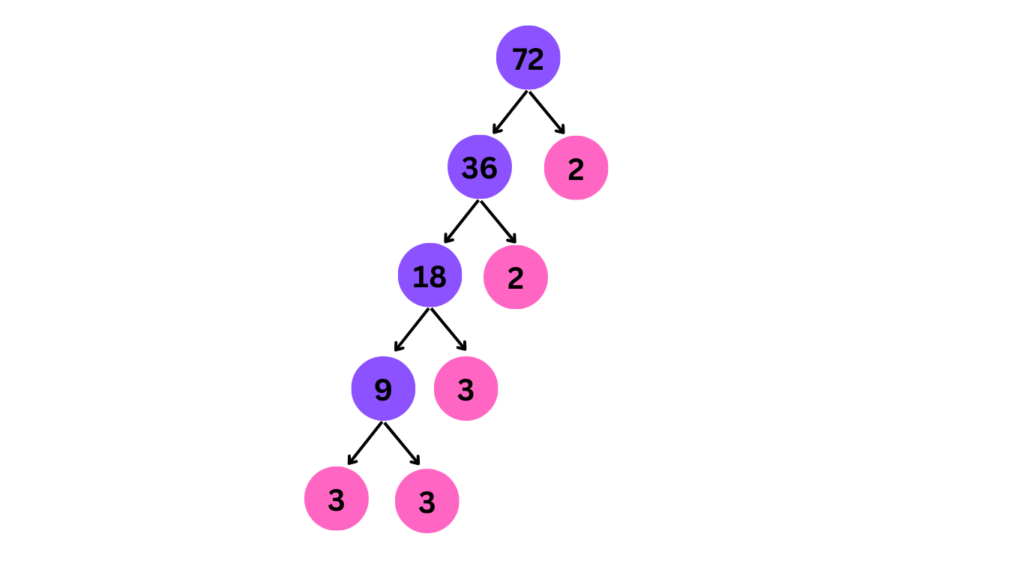
By following the branches from the bottom up, we multiply the prime numbers we encountered: 72 = 2 x 2 x 2 x 3 x 3. We can also express this using exponents, denoting the number of times a prime number appears in the factorization: 72 = 2^3 x 3^2.
Division Method
The division method involves repeatedly dividing the number by its smallest prime factor until you reach 1. Write down each quotient and continue dividing the result.
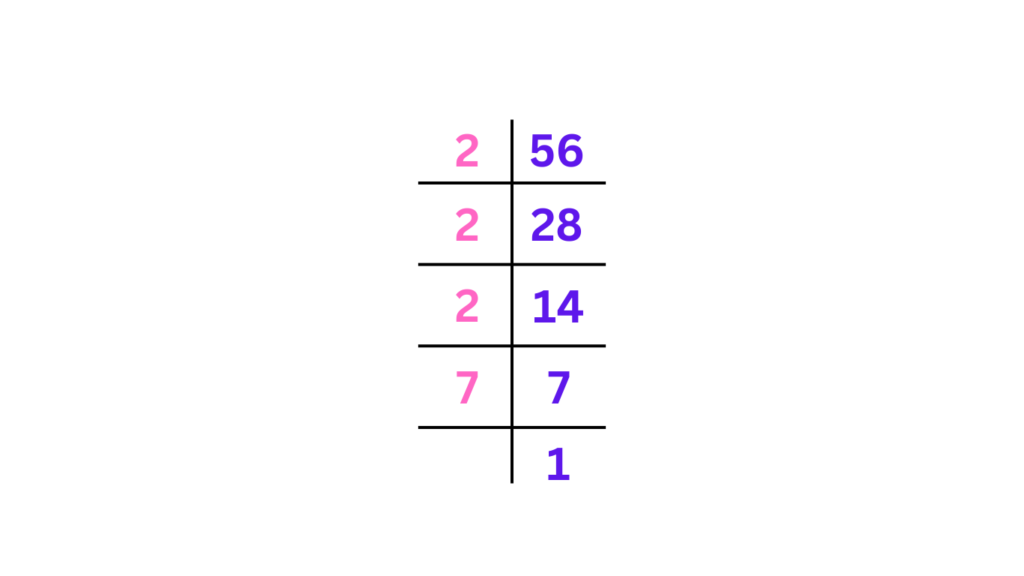
Example: Here is an example of the division method for the number 56.
Step 1: Dividing 56 by the smallest prime number, i.e. 2 in this case. Make sure the prime number exactly divides the number without any remainder.
So, 56÷2=28
Step 2: Again divide the quotient by the smallest prime number, so, in this case, the quotient is 28 and the smallest prime number that can divide it is by 2.
Now, 28÷2=14.
Step 3: We repeat the process of dividing the quotient by the smallest prime number until the quotient becomes 1.
Again, 14÷2=7
Step 4: Since 7 is a prime number, it can only be divided by itself so,
Finally, 7 ÷7 = 1
Therefore, the prime factorization of 56 is 2×2×2×7 or 2^3×7. Here is the visual illustration of how the division method is used:
Applications of Prime Factorization
Mathematics
Prime factorization plays a crucial role in simplifying fractions, finding the greatest common divisor (GCD), and the least common multiple (LCM). For instance, to find the GCD of two numbers, express both in terms of their prime factors and select the smallest power of common primes.
Cryptography
Prime factorization is the backbone of modern encryption methods. Public key cryptography, such as RSA, relies on the difficulty of factoring large composite numbers into their prime factors. This ensures the security of digital communications.
Computer Science
In computer science, prime factorization is used in algorithms and computational problems. It helps in optimizing processes and solving complex mathematical problems efficiently.
Tips and Tricks for Easy Prime Factorization
- Recognizing Prime Numbers Quickly
Familiarize yourself with the list of prime numbers up to at least 100. This can help you quickly identify prime factors.
- Using Prime Factorization Tables
Prime factorization tables list the prime factors of numbers within a range, simplifying the process of breaking down composite numbers.
- Practice Problems
Include a few practice problems to hone your skills:
- Prime factorization of 45.
- Prime factorization of 100.
- Prime factorization of 144.
Solutions:
- 45: 3^2×5.
- 100: 2^3×5^2.
- 144: 2^4×32.
Conclusion
Prime factorization is a fundamental concept that simplifies complex mathematical expressions and has practical applications in various fields. By mastering the steps outlined in this guide, you’ll enhance your math skills, boost your confidence, and be better prepared for real-world applications.
Remember, practice makes perfect, so keep working on those factor trees and division problems to watch your skills grow. If you have any questions or examples you’d like to share, feel free to leave a comment below.
Frequently Asked Questions (FAQs)
What is the prime factorization of a number?
It is the expression of the number as the product of its prime factors. For example, the prime factorization of 28 is 2^3×7.
Why is prime factorization important?
It is crucial for simplifying fractions, finding GCD and LCM, and in fields like cryptography and computer science.
How do you know when to stop factorizing?
When all the remaining factors are prime numbers, you have completed the factorization.