Have you ever wondered how ancient civilizations built their monumental structures? The secret lies in the power of geometry. Geometry is all around us, from the buildings we live in to the art we admire. It’s a branch of mathematics that deals with shapes, sizes, and the properties of space, and it’s been shaping our world for thousands of years. In this article, we’ll dive deep into the fascinating world of geometry, exploring its basics, its different types, its applications, and much more. By the end, you’ll have a new appreciation for the geometric principles that underpin so much of our daily lives.
What Is Geometry?
To start, what is geometry? Geometry is a branch of mathematics concerned with the properties and relations of points, lines, surfaces, and solids. The word “geometry” comes from the Greek words “geo” (earth) and “metron” (measurement). It’s one of the oldest mathematical disciplines, with roots tracing back to ancient civilizations like the Egyptians and Greeks.
Historical Background
The history of geometry is rich and varied. Ancient Egyptians used it for land surveying and construction, notably in building the pyramids. The Greeks, however, took it to new heights. Euclid, often called the “Father of Geometry,” wrote “Elements,” a collection of books that systematically laid out the principles of geometry. Pythagoras, another Greek mathematician, is famous for the Pythagorean theorem, a fundamental principle in geometry. These early contributions laid the foundation for it to study today.
Basic Concepts
To truly understand geometry, we need to familiarize ourselves with its basic concepts. These include points, lines, planes, angles, shapes, and theorems.
Points, Lines, and Planes
- Points: A point is a precise location in space with no dimensions—no length, width, or height. It’s usually represented by a dot.
- Lines: A line is a straight one-dimensional figure that extends infinitely in both directions. It has length but no width or height.
- Planes: A plane is a flat, two-dimensional surface that extends infinitely in all directions. It has length and width but no height.
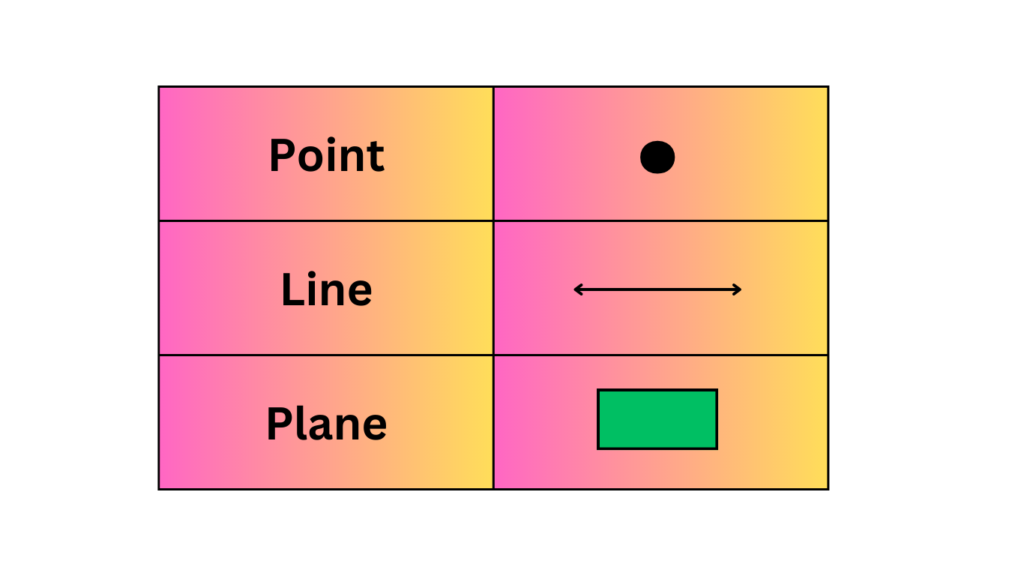
These basic elements form the building blocks of all geometric shapes and figures.
Angles
Angles are formed by two rays (or line segments) that share a common endpoint, called the vertex. Angles are measured in degrees.
- Acute Angle: The angles that are less than 90 degrees are called acute angles.
- Right Angle: The angles that are exactly 90 degrees are called right angles.
- Obtuse Angle: The angles that are between 90 and 180 degrees are called obtuse angles.
- Straight Angle: The angles that are exactly 180 degrees are called straight angles.
Angles are fundamental in geometric concepts because they help define the properties and relationships of shapes and figures.
Shapes and Figures
There are generally two types of shapes and figures in geometric concepts.
- 2D Shapes: These include circles, triangles, squares, rectangles, and polygons. They have length and width but no height.
- 3D Shapes: These include cubes, spheres, cylinders, and pyramids. They have length, width, and height.
Understanding the properties of these shapes is crucial for solving geometric problems and understanding the world around us.
Theorems and Proofs
Theorems are statements that can be proven based on previously established statements and accepted mathematical principles. Proofs are logical arguments that demonstrate the truth of a theorem.
- Pythagorean Theorem: In a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
- Euclid’s Postulates: These are the basic assumptions on which Euclidean geometry is based, such as “a straight line can be drawn from any point to any other point.”
Theorems and proofs are essential because they provide a structured way to understand and demonstrate the properties of geometric figures.
Types of Geometry
Geometry is not just limited to the basic concepts we’ve discussed. It has several types, each with its own principles and applications.
Euclidean Geometry
Euclidean geometry, named after Euclid, is the study of flat space. It deals with the properties and relationships of points, lines, and shapes in a two-dimensional plane or three-dimensional space.
- Principles: Based on Euclid’s postulates, such as the idea that parallel lines never meet.
- Applications: Used in everyday life, engineering, architecture, and more.
Non-Euclidean Geometry
Non-Euclidean geometry explores spaces that are not flat. There are two main types:
- Hyperbolic Geometry: Deals with saddle-shaped spaces where parallel lines can diverge.
- Elliptic Geometry: Deals with spherical spaces where parallel lines can converge.
They are essential in fields like astronomy and physics, where the shapes of spaces and surfaces are not always flat.
Analytic Geometry
Analytic geometry, also known as coordinate geometry, uses algebra to represent and solve geometric problems. It involves using coordinates and equations to describe geometric figures.
- Principles: Combines algebra and geometry through the use of Cartesian coordinates.
- Applications: Widely used in calculus, physics, engineering, and computer graphics.
Differential Geometry
Differential geometry uses calculus and algebra to study the properties of curves and surfaces.
- Principles: Focuses on concepts like curvature and torsion.
- Applications: Critical in fields like physics, especially in the theory of relativity and the study of spacetime.
Applications of Geometry
Geometry is not just a theoretical field; it has practical applications in many areas of our lives.
Architecture and Engineering
It is fundamental in architecture and engineering. It helps in the design and construction of buildings, bridges, and other structures.
- Building Design: Architects use geometric principles to create blueprints and plans. Shapes like triangles and rectangles provide stability and strength.
- Structural Integrity: Engineers use geometry to calculate forces, angles, and dimensions, ensuring structures are safe and sound.
Famous examples of geometric principles in architecture include the pyramids of Egypt, the Parthenon in Greece, and modern skyscrapers.
Art and Design
Artists and designers often use geometric shapes and principles in their work.
- Graphic Design: Geometric shapes are used to create layouts, logos, and illustrations.
- Fashion Design: Designers use geometric patterns and shapes in clothing and accessories.
Historical examples include its uses in Islamic art, with its intricate tile patterns, and the works of artists like Piet Mondrian, who used geometric shapes to create abstract art.
Everyday Life
Geometry is present in many aspects of our daily lives.
- Household Items: Objects like tables, chairs, and books are often rectangular or square.
- Sports: Fields and courts, such as soccer fields and basketball courts, are designed using geometric principles.
- Nature: Patterns in nature, like the hexagonal shapes of honeycombs and the spiral shapes of shells, follow geometric principles.
Understanding geometry helps us make sense of the shapes and patterns we encounter every day.
Technology and Robotics
In the world of technology, geometry plays a crucial role.
- Computer Graphics: It is used to create realistic 3D models and animations in video games and movies.
- Robotics: Robots use geometric principles to navigate and interact with their environment. For example, robotic arms use geometry to determine the angles and movements needed to pick up objects.
In artificial intelligence and machine learning, geometric algorithms help in image recognition and other complex tasks.
The Role of Geometry in Science
the geometric concept is not just confined to mathematics; it’s a vital tool in various scientific fields.
Physics
In physics, the geometric concept is used to describe the shapes and properties of objects and spaces.
- Theories and Models: Geometric principles help physicists develop models and theories, such as Einstein’s theory of relativity, which describes the curvature of spacetime.
- Measurements: It is used to measure and calculate physical properties like area, volume, and density.
Astronomy
Astronomers use geometric concepts to study the shapes and movements of celestial bodies.
- Celestial Mechanics: It helps astronomers calculate the orbits of planets and the shapes of galaxies.
- Space Exploration: Geometric principles are used to design spacecraft and plan missions.
Biology
The geometric concept is also present in biology, where it helps scientists understand the shapes and structures of living organisms.
- Patterns in Nature: Geometric patterns, such as the spirals of shells and the fractal patterns of leaves, are studied to understand growth and development.
- DNA Structure: The double helix structure of DNA is a geometric shape that is crucial to understanding genetics.
Learning Geometry
Understanding geometric concepts is an essential skill that provides numerous benefits.
Educational Importance
It is a core component of the school curriculum for good reason.
- Problem-Solving Skills: Studying geometric concepts helps develop logical thinking and problem-solving skills.
- Spatial Awareness: It improves spatial reasoning, which is crucial for understanding the physical world.
Tips for Learning Geometry
Here are some tips to help you master geometric concepts:
- Practice Regularly: Work on different types of problems to strengthen your understanding.
- Use Visual Aids: Draw diagrams and use models to visualize geometric concepts.
- Relate to Real Life: Find examples of geometric principles in everyday objects to make learning more engaging.
- Seek Help: Don’t hesitate to ask for help from teachers or use online resources.
Practical exercises and real-world applications can make learning geometric concepts more enjoyable and effective.
Fun Facts About Geometry
Let’s explore some fun and fascinating facts about geometry.
Historical Anecdotes
The study of geometric concepts has a rich history full of interesting stories.
- Pythagoras and the Beans: Legend has it that Pythagoras, the famous mathematician, had a strange aversion to beans. He believed that beans contained the souls of the dead.
- Archimedes and the King’s Crown: Archimedes, a Greek mathematician, used geometric principles to determine whether a crown was made of pure gold. He discovered the principle of buoyancy, leading to his famous exclamation, “Eureka!”
Geometric Curiosities
Geometric concepts are full of fascinating shapes and properties.
- The Möbius Strip: This is a surface with only one side and one edge. It’s a great example of a geometric curiosity that defies our usual understanding of shapes.
- Fractals: These are complex geometric shapes that can be split into parts, each of which is a reduced-scale copy of the whole. They appear in nature, such as in snowflakes and coastlines.
Mathematical Challenges
Geometry also includes some famous puzzles and problems.
- The Four-Color Theorem: This theorem states that any map can be colored using just four colors, such that no two adjacent regions share the same color.
- Kepler’s Conjecture: This problem, posed by Johannes Kepler in 1611, is about the most efficient way to pack spheres. It wasn’t proven until 1998!
Conclusion
Geometry is a fascinating and essential branch of mathematics that plays a crucial role in our world. From ancient monuments to modern technology, it helps us understand and shape our environment. By learning about the basic concepts, different types, and wide-ranging applications of geometry, we gain valuable insights into both the mathematical and physical worlds.
So next time you look at a building, a piece of art, or even a leaf, remember the geometric principles at play and appreciate the beauty and utility of this timeless field of study. Share your thoughts, ask questions, and dive deeper into it—you’ll find it’s more than just shapes and lines; it’s a powerful tool that unlocks the mysteries of our universe.
Frequently Asked Questions (FAQs)
What is geometry?
Geometry is the branch of mathematics that deals with the properties and relationships of points, lines, surfaces, and solids.
Why is geometry important?
Geometry is essential for understanding and solving problems related to space and shape. It has practical applications in fields like architecture, engineering, art, and science.
Who is known as the father of geometry?
Euclid, a Greek mathematician, is often referred to as the father of geometry due to his influential work “Elements.”
What are some essential geometric theorems?
Key theorems include the Pythagorean theorem and Euclid’s postulates.
What is the difference between 2D and 3D shapes?
2D shapes have length and width but no height (e.g., squares, circles). 3D shapes have length, width, and height (e.g., cubes, spheres).