Introduction
Have you ever wondered what happens when two lines meet? Let’s dive into the fascinating world of intersecting lines. From the streets we walk on to the designs of buildings around us, intersecting lines are all around. This article will guide you through the ins and outs of intersecting lines, their properties, types, applications, and more. Buckle up for an exciting geometric journey.
What are Intersecting Lines?
Imagine two paths converging at a crossroads. That’s the essence of intersecting lines – lines that meet or cross each other at a single point. Just like those paths guiding you to your destination, intersecting lines create a specific point of connection in the world of geometry.
In simpler terms, intersecting lines are two or more lines that meet or cross at a single point. This point is known as the point of intersection. It’s a simple concept but holds great significance in geometry and real-life applications.
To solidify this concept, take a look at the image below:
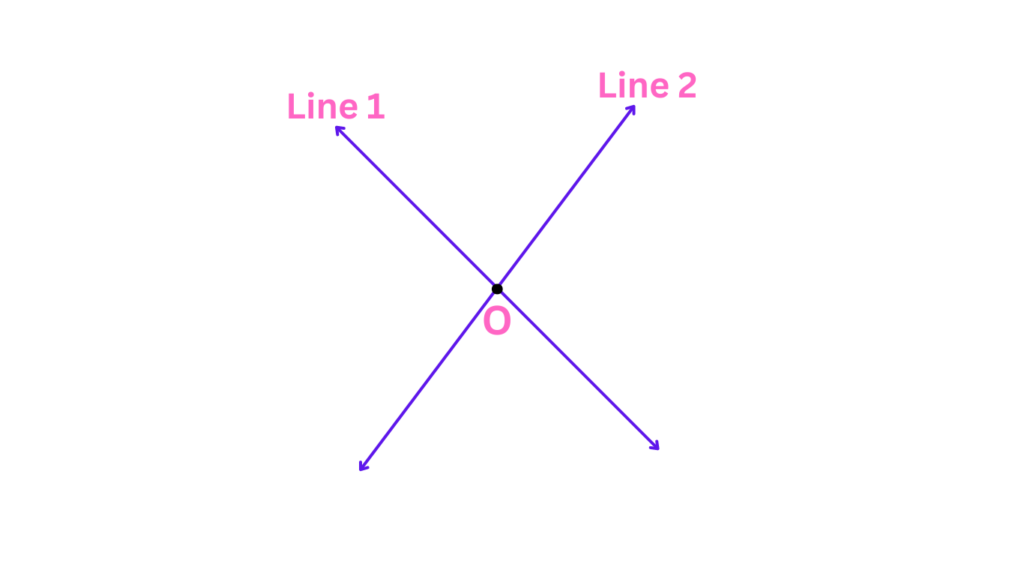
As you can see, Line 1 and Line 2 intersect at a single point, i.e. point of intersection, clearly marked in the image. This point of intersection is where the magic happens – it’s the bridge connecting the two separate lines.
Properties of Intersecting Lines
Now that you’ve met the different types of intersecting lines, let’s delve deeper into their defining characteristics. These properties are the building blocks that make intersecting lines unique:
-
The One and Only Intersection Point: Unlike a crowded party with multiple guests arriving, intersecting lines only meet at one specific location known as a point of intersection. Imagine two highways – they can only cross paths at a designated intersection point. This exclusivity is a key feature of intersecting lines.
-
Opposite Angle Allies: When lines intersect, they create a fascinating dance of angles around the meeting point. Here’s a cool twist: opposite angles (angles directly across from each other) always add up to 180 degrees. Think of traffic lights at an intersection – a green light (one angle) means a red light (opposite angle) to ensure smooth traffic flow (180 degrees of control over the intersection). This property of opposite angles being supplementary is a hallmark of intersecting lines.
Types of Intersecting Lines
Not all intersections are created equal. They can come in different flavors, each with its own unique angle on the world. Here’s a closer look at the most common types:
-
Perpendicular Lines: These are the A-listers of the intersecting line world. Perpendicular lines meet at a perfect 90-degree angle, creating a crisp right angle. Imagine a perfect “L” shape – that’s the signature look of perpendicular lines. They ensure perfect alignment and straight edges, which is why they’re often used in construction and design.
-
Acute Lines: These lines intersect at an angle less than 90 degrees, creating a sharper “V” shape. Picture two pointy arrows meeting tip-to-tip – that’s the essence of acute lines. They add a dynamic element to geometric shapes and can be found in various applications, from roof designs to arrowheads.
-
Obtuse Lines: These lines intersect at an angle greater than 90 degrees but less than 180 degrees, resembling a wider “U” shape. Think of two roads merging at a gentle curve – that’s a classic example of obtuse lines. They provide a sense of openness and can be used to create rounded shapes or depict gradual transitions.
Real-World Applications
The beauty of geometry lies in its ability to translate into the real world. Intersecting lines are no exception! Here are some surprising places where you might encounter them:
- Urban Planning and Road Intersections: City planners use these lines to design roadways and intersections. The efficiency and safety of traffic flow depend heavily on how these intersections are designed. Roundabouts, four-way stops, and traffic signals all rely on the principles of intersecting lines.
- Architecture and Design: Architects use these lines to create blueprints and structural designs. The angles and intersections ensure that buildings are both aesthetically pleasing and structurally sound. Think of the intersecting lines in the framework of a skyscraper or the intricate designs of a Gothic cathedral.
- Graphs and Data Visualization: The world of science relies heavily on data visualization. These lines are often used in charts and graphs to plot data points, allowing us to see trends and relationships between variables, such as equilibrium in supply and demand curves in economics.
How to Identify Intersecting Lines
Feeling ready to become an intersecting line pro? Here’s a simple guide to help you identify them in the wild:
-
The Point of No Return (Well, One Point!): The first and foremost sign of intersecting lines is the presence of a single point of intersection. Look for two lines that meet or cross each other at a specific location.
-
Parallel Pals or Intersecting Allies?: Once you’ve identified a potential meeting point, take a closer look at the lines themselves. Are they truly intersecting (crossing each other) or simply running parallel (side-by-side)?
-
The Ruler Trick: If you’re unsure, imagine extending the lines with a ruler or a straightedge. If they would eventually meet at a single point if extended infinitely, then congratulations, you’ve found intersecting lines.
By following these simple steps, you’ll be a master of spotting these lines in no time. So, the next time you’re looking at a building, a graph, or even a simple crossroads, see if you can identify the magic of intersecting lines at play.
Angles Formed by Intersecting Lines
For those who want to take their geometric knowledge a step further, let’s explore the specific angles formed by intersecting lines. Understanding these different angles can add depth to understanding these lines and their relationship with angles in geometry.
-
Vertical Angles: When two lines intersect, they form two pairs of opposite angles called vertical angles. These angles are always equal. For instance, if two lines intersect and form angles of 30° and 150°, the opposite angles will also be 30° and 150°, respectively. See the angles p, q, r, and s in the picture below. The angle ‘p’ will always be equal to its opposite angle, ‘q’, i.e. p = q, and angle ‘r’ will always be equal to angle ‘s’.
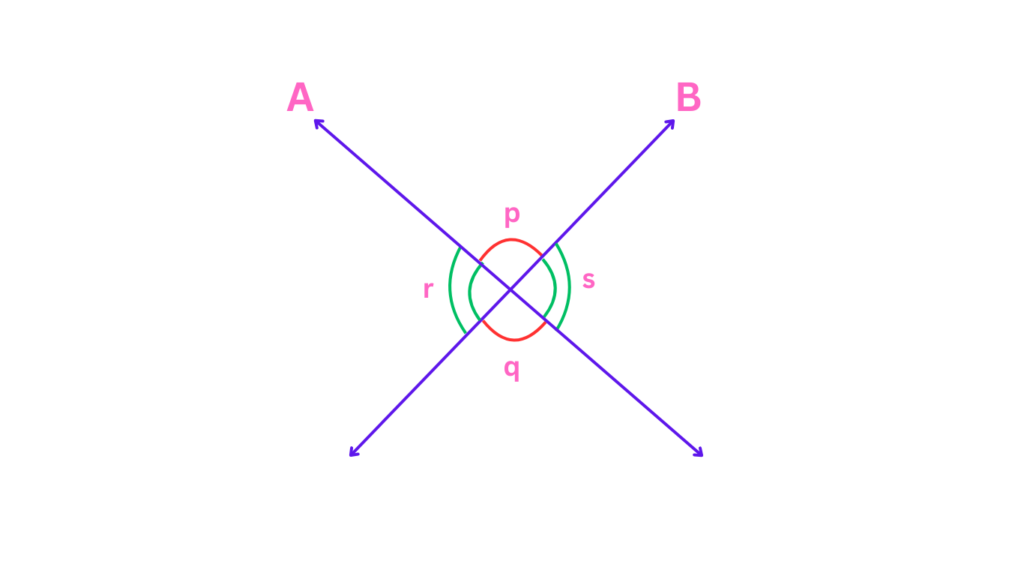
-
Adjacent Angles: These are angles that share a common side and a common vertex. When two lines intersect, the adjacent angles add up to 180°. This is known as the Linear Pair Postulate. You can look in the picture above, the sum of angles ‘p’ and ‘r’ or angles ‘s’ and ‘q’ will always be 180 degrees, i.e. p + q = 180 degrees, and s + q = 180 degrees.
Fun Facts
Let’s add a dash of trivia to your geometric knowledge. Here are some interesting facts about intersecting lines:
- The Word on the Street: The word “intersect” comes from the Latin word “intersectare,” meaning “to cut across or divide.” It perfectly captures the essence of these lines – two entities meeting and creating a point of division.
- Parallel Lines: Imagine two train tracks running side-by-side, forever destined to remain parallel. That’s the story of parallel lines. No matter how far you extend them, they will never intersect. They’re the loners of the line world, maintaining a constant distance but never truly connecting.
Conclusion
Intersecting lines are more than just a basic geometric concept; they are fundamental to understanding and interpreting the world around us. From the angles they form to their real-world applications, they play a crucial role in various fields. By understanding what they are and how they work, we can better appreciate the complexity and beauty of geometry in everyday life. So next time you cross the street or look at a building, take a moment to think about the intersecting lines that make it all possible. Keep exploring the geometric world around you, and you’ll find they are indeed powerful and fascinating.
Frequently Asked Questions (FAQs)
What Are Intersecting Lines in Geometry?
Intersecting lines are two or more lines that cross each other at a single point. This point is known as the point of intersection.
Can lines intersect at more than one point?
No, by definition, intersecting lines meet at only one point. If two lines appear to meet at multiple points, they might actually be multiple line segments or even a single, curvy line.
How Are Intersecting Lines Used in Everyday Life?
Intersecting lines are used in urban planning, architecture, and even in graphs to represent data. They are essential for designing roadways, and buildings, and interpreting data visually.