The Rhombus Shape – Unveiling the Secrets of the 4-Sided Wonder

Introduction

Geometry is a realm of shapes and figures that captivate the mind with their symmetry and elegance. Among these geometric wonders, the rhombus shape stands out as a sparkling gem, showcasing unique properties and mesmerizing characteristics. In this article, we will delve into the enchanting world of the rhombus shape, exploring its definition, properties, and the fascinating concept of the area of a rhombus. Whether you’re a student seeking to deepen your understanding of geometry or simply intrigued by the beauty of shapes, this article is for you.

What is a Rhombus Shape?

Imagine a kite – that childhood symbol of soaring dreams and carefree adventures. Now, picture it with a touch of elegance, its sides all equal in length and its opposite sides running parallel to each other. That, my friends, is the essence of a rhombus shape.

In simpler terms, a rhombus is a flat, four-sided figure (also known as a quadrilateral) where all four sides have equal lengths. But there’s more to it than just equal sides. The defining characteristic of a rhombus lies in its parallel opposite sides. Think of train tracks running side-by-side, forever maintaining the same distance between them. That’s the kind of parallelism we’re talking about here.

To solidify this concept, take a look at the image below:

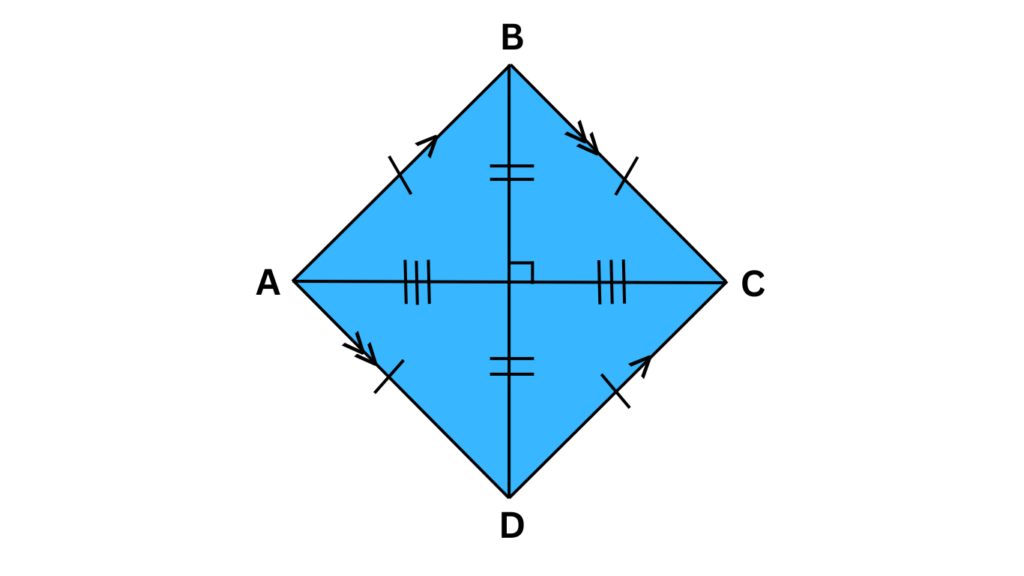
As you can see, the rhombus has four sides of equal length, labeled here for clarity. Notice how sides AB and CD, as well as sides AD and BC, run strictly parallel to each other. This parallel magic is a key feature that sets the rhombus apart from other quadrilaterals.

Properties of a Rhombus Shape

Now that we’ve grasped the basic idea of a rhombus shape, let’s delve deeper and unveil its fascinating properties. These characteristics are like the building blocks that define the unique identity of a rhombus shape:

• Sides: The defining feature of a rhombus is that all four of its sides are of equal length. This property is what gives the rhombus its symmetrical shape and sets it apart from other quadrilaterals like parallelograms and rectangles, where only opposite sides are equal.
• Diagonals: Imagine drawing a line from one corner of the rhombus to the opposite corner. These lines, which intersect (cross each other) inside the shape, are called diagonals. Here’s the surprising twist: in a rhombus, these diagonals bisect each other at a perfect 90-degree angle. That’s right, a crisp right angle just like the corner of a well-made book.
• Opposite Angles: Remember those parallel sides we discussed earlier? Well, they bring another interesting property to the table. In a rhombus, opposite angles (think of the angles where two sides meet) are always congruent, meaning they have exactly the same measure. So, if you measure one angle, you automatically know the measure of its opposite counterpart.

Is Square a Rhombus?

Yes! A square is actually a rhombus. Surprise! A square can actually be considered a special type of rhombus. Why? Because a square fulfills all the defining characteristics of a rhombus – four equal sides and opposite sides running parallel. However, a square goes a step further by having all four angles measure exactly 90 degrees (right angles). So, while all squares are rhombi, not all rhombi are squares. The world of rhombi isn’t confined to just one kind. Just like snowflakes, these shapes can exhibit some fascinating variations.

Similarly, this one might sound a bit complex, but it’s actually quite interesting. An isosceles trapezoid is a quadrilateral with one set of parallel sides (like a regular trapezoid) and two non-perpendicular diagonals. Now, if this trapezoid also happens to have all four sides equal in length, then it transforms into a special type of rhombus – the isosceles trapezoid rhombus!

How to Draw a Rhombus Shape

Feeling inspired to create your own rhombus masterpiece? Here’s a step-by-step guide to help you become a rhombus shape-drawing pro:

Method 1: Using a Compass and Ruler

1. Gather your tools: You’ll need a compass, a ruler, and a pencil.
2. Draw a baseline: Use your ruler to draw a straight line of any desired length. This will be the base of your rhombus.
3. Mark the center: Carefully locate the midpoint of the baseline using your ruler. Mark this point with a small dot.
4. Set your compass: With the compass point placed on the center dot, adjust the other leg to match half the desired length of your rhombus side (remember, all sides in a rhombus are equal).
5. Draw the first two sides: Using the compass setting, draw two arcs from the center point, one above and one below the baseline, intersecting the line at both ends. These arcs will create the two sides of your rhombus.
6. Connect the dots: Now, use your ruler to connect the top two points where the arcs intersect and the two endpoints you marked on the baseline. This will form the first two sides of your rhombus.
7. Repeat for the other sides: With the same compass setting, repeat steps 4 and 5, but this time create arcs that intersect the already drawn sides at their midpoints. This will define the top and bottom sides of your rhombus.
8. Connect and complete: Finally, connect the endpoints of the newly drawn arcs with straight lines using your ruler. This will complete your rhombus shape.

Method 2: Using Online Geometry Tools

The digital age offers a convenient alternative! Numerous online geometry tools allow you to create and manipulate shapes like rhombi. These tools often provide user-friendly interfaces where you can simply input the desired side length and manipulate the shape on the screen. This can be a great way to experiment with different rhombus sizes and explore their properties visually.

Calculating the Area and Perimeter of a Rhombus

Now that you can confidently draw a rhombus shape, let’s delve into the world of measurement. We can calculate two important aspects of a rhombus: its area and its perimeter.

Area

The area of a shape refers to the amount of space it occupies. For a rhombus, calculating the area is quite straightforward. The area of a rhombus can be calculated using the lengths of its diagonals with the following formula:

Area of Rhombus = (1/2) * Diagonal 1 * Diagonal 2​

This formula is derived from the fact that the diagonals of a rhombus intersect at right angles, dividing it into four right-angled triangles. By calculating the area of these triangles and summing them, we arrive at the formula for the area of the rhombus.

Example Calculation

Let’s calculate the area of a rhombus with diagonals of 10 cm and 8 cm:

Area = (1/2) * 10cm * 8cm

Area = (1/2) * 80 square centimeters

Area = 40 square centimeters

Perimeter

The perimeter, on the other hand, refers to the total length of all the sides of a shape added together. Since all sides of a rhombus are equal, calculating the perimeter is simple. Here’s the formula:

Perimeter of a Rhombus = 4 x side length

This formula multiplies the side length by 4, effectively adding up the lengths of all four equal sides.

Example Calculation

For a rhombus with each side measuring 5 cm:

Perimeter = 4 * 5cm

Perimeter = 20cm

Real-Life Applications of the Rhombus Shape

Architecture

The rhombus shape is widely used in architecture for its aesthetic appeal and structural properties. The shape can be seen in various building designs, including floor tiles and window designs. The rhombus shape adds a dynamic visual interest and strength to structures.

Art and Design

In art and design, the rhombus shape is often used to create intricate patterns and designs. Artists and designers use the symmetry and unique properties of the rhombus to create visually stunning works. For instance, the famous Penrose tiling, a type of non-repeating tiling, often incorporates rhombuses.

Everyday Examples

Rhombuses can be found in various everyday objects. For example:

• Kites: Many kites are shaped like rhombuses.
• Jewelry: Some gemstones are cut in a rhombus shape to enhance their brilliance.
• Road Signs: Certain road signs, especially those indicating warning or caution, are often shaped like rhombuses.

Conclusion

The rhombus shape might seem simple at first glance, but it holds a wealth of interesting properties and practical applications. From ancient geometry to modern architecture and design, rhombuses play a vital role in our understanding of the world. By mastering the concepts and calculations related to rhombuses, you can appreciate their beauty and utility in everyday life and beyond. So next time you see a rhombus-shaped object, you’ll know just how fascinating it truly is.

If you have any thoughts, questions, or rhombus sightings to share, leave a comment below. Let’s continue the geometric adventure together.

Frequently Asked Questions (FAQs)

What makes a rhombus shape unique compared to other quadrilaterals?

A rhombus is distinct from other quadrilaterals due to its equal side lengths and diagonals that bisect each other at right angles. These properties set the rhombus apart as a symmetrical and balanced shape.

How can the area of a rhombus be calculated if the lengths of the diagonals are known?

By using the formula (Diagonal 1 x Diagonal 2) / 2, the area of a rhombus can be determined with precision. This formula leverages the relationship between the diagonals to calculate the total enclosed area of the rhombus.

What practical applications does the rhombus shape have in real-world scenarios?

The rhombus shape is utilized in fields like architecture, engineering, and design for creating aesthetically pleasing layouts, optimizing space utilization, and enhancing structural stability. Its symmetrical properties make it a valuable tool in various practical applications.