Have you ever encountered a puzzling equation with a cube root symbol (∛) and scratched your head?
Well, fret no more! This article is your one-stop guide to understanding cube roots, from their fundamental concept to their surprising applications in the real world. Whether you’re a student seeking to conquer math exams or simply someone curious about the wonders of numbers, this exploration is designed for you.
What are Cube Roots?
Imagine a number that, when multiplied by itself three times in a row (like building a cube with identical sides), gives you another specific number. That magical number you started with is the cube root of the final result. We use the fancy symbol ∛ (read as “cube root of”) to represent this operation.
For instance, the cube root of 27 (written as ∛27) is 3. Why? Because 3 x 3 x 3 = 27. Here, the number 3 is the root you need to multiply three times to get 27, the perfect cube.
Now, you might be thinking, “Isn’t this similar to square roots?” You’re absolutely right! A square root finds a number that, when multiplied by itself twice (like creating a square with equal sides), gives you another number. So, the key difference lies in the number of multiplications – three for cubes and two for squares.
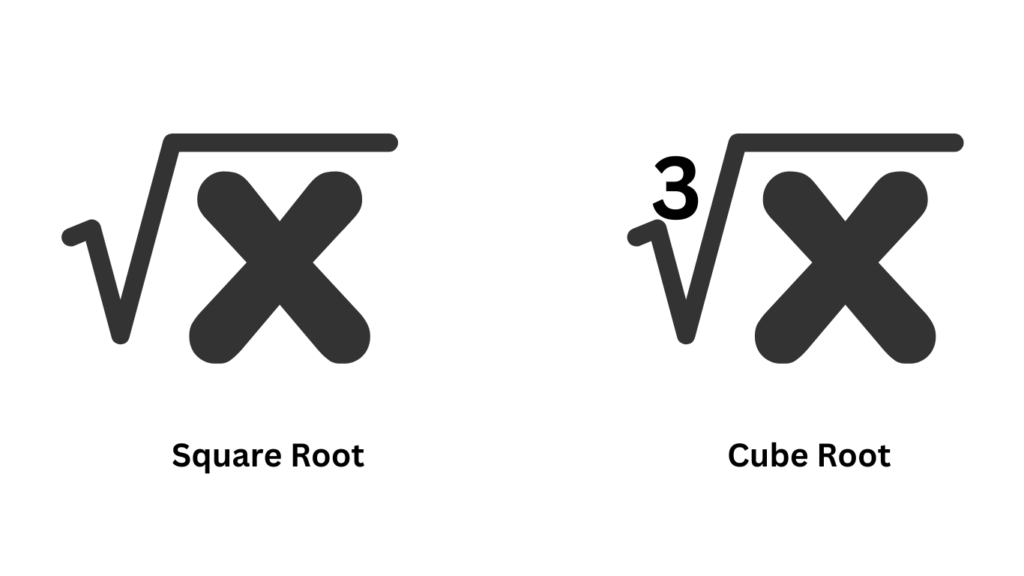
Here’s another crucial distinction: perfect cubes. These are numbers that can be obtained by multiplying an integer by itself three times. Examples include 1 = (1 x 1 x 1), 8 = (2 x 2 x 2), and 64 = (4 x 4 x 4). Not all numbers are perfect cubes, though. Numbers like 10 or 15 don’t fit this mold, and their cube roots are what we call irrational numbers. These numbers cannot be expressed as a simple fraction and have infinitely many decimal places that never repeat.
How to Find Cube Roots
Conquering cube roots can be an exciting adventure! Here, we’ll explore some key methods to unveil these elusive values:
1. Listing Perfect Cubes: This is a great strategy for smaller numbers. Simply create a list of perfect cubes (1, 8, 27, 64, and so on) and see if your target number falls neatly within the list. If it does, its cube root is the corresponding integer.
Example: If we are asked to find the cube root of 27.
Following the method, we check our list of perfect cubes. We find that 27 is indeed on the list. Therefore, the cube root of 27 is 3, because 3 x 3 x 3 = 27.
2. Prime Factorization: This method delves a bit deeper into number theory. By breaking down a number into its prime factors (the building blocks of any number), you can identify perfect cubes. If a number has each prime factor appearing in groups of three, it’s a perfect cube, and its cube root is easily determined from the prime factors.
Example: If we are asked to find the cube root of 64.
Prime factorize 64: 64 = 2 x 2 x 2 x 2 x 2 x 2 (six twos). Here, since we have six twos, which can be grouped perfectly into three sets of two (2 x 2 x 2), we know 64 is a perfect cube. The cube root of 64 is simply the product of the cube root of each prime factor, which in this case is 2 x 2 x 2, or 8.
3. Estimation: Now, what if we don’t have the exact cube root? No worries! Estimation can be your friend. Locate perfect cubes close to your target number. If your number is closer to a larger perfect cube, its cube root will be slightly higher than the root of the smaller one. This approach provides a good starting point for further calculations.
Example: If we need to estimate the cube root of 125.
Looking at our list of perfect cubes, we see that 125 falls between 64 (4 x 4 x 4) and 128 (2 x 2 x 2 x 2 x 2 x 2). Since 125 is closer to 128, we know its cube root will be slightly higher than 4 (the cube root of 64). This estimation helps us narrow down the answer and can be a valuable tool when dealing with larger numbers.
4. Calculators and Root Tables: The final way of calculating it is using the calculators and the root tables. This is an easy process but while technology can provide instant answers, relying solely on calculators or pre-made cube root tables hinders a deeper understanding. These tools are valuable for quick checks. First, we can find the answer using one of the above techniques and then check our answers in a calculator or table to know whether the answer is correct or not. But remember the true learning lies in the methods explained above.
Applications of Cube Roots: From Tiny Boxes to Vast Universes
Cube roots aren’t just mathematical concepts confined to textbooks. They have a surprising range of applications in our everyday world:
1. Volume Calculations: Have you ever wondered how much space a cubic box can hold? Cube roots come into play here! To find the volume of a cube (the amount of space it occupies), you simply cube (multiply three times) the side length. If the side length is represented by the variable “s,” the volume (V) is calculated as V = s x s x s. However, what if the side length isn’t a whole number? Here’s where the cube root shines! By taking the cube root of the known volume, you can determine the side length of the cube. This principle extends to other cubic shapes as well.
2. Beyond the Box: Cube roots extend far beyond the realm of calculating perfect cube volumes. Here are some intriguing examples of how they find application in various scientific and engineering disciplines:
Chemistry: In the fascinating world of chemistry, it plays a role in analyzing the structure of crystals. The arrangement of atoms in crystals often follows specific geometric patterns. By understanding the lengths of these arrangements, scientists can utilize them to determine the unit cell size, a fundamental building block of a crystal’s structure. This knowledge is crucial for understanding the properties of materials and developing new ones with desired characteristics.
Engineering: Efficiency is key in engineering, and it comes into play when designing storage containers. Imagine a company needs to create boxes to hold a specific volume of product. By utilizing the cube root of the desired volume, engineers can determine the optimal side length for the boxes, minimizing wasted space and maximizing storage capacity. This principle applies to everything from designing shipping containers to planning efficient warehouse layouts.
The applications of cube roots in science and engineering are vast and ever-expanding. From calculating fluid flow rates in hydraulic engineering to analyzing the surface area of spherical objects in biology, these mathematical tools play a vital role in various fields. As scientific research delves deeper, we can expect to discover even more fascinating applications of cube roots in the future.
Beyond the Basics: Advanced Concepts and Innovations
Advanced Mathematics
As we venture into higher levels of mathematics, cube roots become stepping stones to even more complex ideas. Here are a couple of examples:
- Higher-order Roots and Their Significance: Cube roots are just the beginning. We can find roots of any order. Square roots (fourth root), fifth roots, and so on, are all calculated using similar principles but with different exponents in the multiplication process. Understanding higher-order roots is crucial in solving complex equations and exploring advanced mathematical concepts like complex numbers.
- Calculus and Mathematical Modeling: Calculus, the study of change, heavily relies on understanding the roots of various orders. Cube roots play a role in finding rates of change, optimizing shapes, and analyzing curved surfaces. Additionally, mathematical modeling, which uses math to represent real-world phenomena, often incorporates them in areas like fluid dynamics (movement of fluids) and heat transfer calculations.
Innovations in Computational Mathematics
The quest to solve complex mathematical problems faster and more efficiently has led to exciting innovations in computational mathematics. Algorithms specifically designed to calculate cube roots and other higher-order roots have been developed. These advancements allow mathematicians and scientists to tackle problems that were previously too cumbersome to solve by hand.
Cutting-edge Research and Applications
The world of mathematics is constantly evolving, and cube roots continue to find new applications in various fields:
- Fractals: These self-similar geometric patterns, often found in nature, can be analyzed and described using higher-order roots.
- Chaos Theory: This branch of mathematics explores unpredictable systems. Cube roots can help model and understand chaotic behavior in areas like weather patterns or population dynamics.
- Cryptography: The world of secure communication relies heavily on complex mathematical problems. Cube roots, along with other roots, can be incorporated into encryption algorithms to safeguard sensitive information.
Future Trends and Developments
As computing power increases and mathematical research delves deeper, we can expect even more exciting discoveries related to cube roots and their applications. For instance, the exploration of higher-dimensional spaces might involve calculations with even more complex roots, building upon the foundation laid by it.
Conclusion
By now, you’ve hopefully gained a solid understanding of cube roots, their calculation methods, and their diverse applications. Remember, they are not just mathematical curiosities; they are powerful tools that unlock solutions in various fields. Whether you’re a student seeking to master math concepts or simply someone curious about the world around you, appreciating its significance opens doors to a deeper understanding of the fascinating world of numbers.
Feel free to explore further and practice! There are numerous online resources and practice problems available to solidify your grasp of this valuable mathematical concept.
Frequently Asked Questions (FAQ)
1. How can I tell if a number is a perfect cube?
A perfect cube will have each of its prime factors appearing in groups of three. For example, 27 (3 x 3 x 3) is a perfect cube because the prime factor 3 appears three times.
2. What if the cube root of a number is not a whole number?
As we saw, not all numbers are perfect cubes. In such cases, the cube root will be an irrational number with an infinite number of decimal places that never repeat. Calculators can provide an approximation.
3. Are there any real-world examples of cube roots beyond volume calculations?
Absolutely! Cube roots are used in various fields. For instance, they play a role in calculating the packing efficiency of spheres (how efficiently spheres can be packed together in a container) and analyzing the growth rates of certain biological populations.