Introduction
Integers are the building blocks of mathematics, forming a rich tapestry of numbers that extend infinitely in both positive and negative directions. In this article, we will embark on a journey to unlock the magic of integers and explore the fascinating world of mathematical possibilities that they offer. From basic definitions to advanced applications, we will delve deep into its realm and discover the beauty and complexity that lies within.
Whether you’re a student looking to enhance your understanding of integers or a math enthusiast eager to explore new concepts, this article is designed to be your comprehensive guide to the captivating world of integers.
Understanding Integers
What are Integers?
Integers are whole numbers that can be positive, negative, or zero. They do not have any fractional or decimal parts. Examples include -3, -2, -1, 0, 1, 2, 3, and so on.

Is 0 an Integer?
Yes, 0 is an integer. While zero may seem like a special case due to its neutral position between positive and negative numbers, it is indeed classified as an integer. Zero plays a crucial role in mathematics, serving as the additive identity element in arithmetic operations.
Properties of Integers
Positive Integers:
- Greater than zero: Positive integers are numbers greater than zero.
- Denoted without a sign: Positive integers are typically written without a positive sign (+).
Negative Integers:
- Less than zero: Negative integers are numbers less than zero.
- Denoted with a negative sign: Negative integers are written with a negative sign (-) before the number.
Zero:
- Neutral element: Zero serves as the neutral element in arithmetic operations, where adding or subtracting zero does not change the value of a number.
- Neither positive nor negative: Zero is unique in that it is neither positive nor negative.
Importance of Integers
Integers play a vital role in various mathematical concepts and real-world applications. Understanding them is essential for:
Basic Arithmetic Operations
At the heart of everyday mathematics lies the necessity to perform basic arithmetic operations—addition, subtraction, multiplication, and division. Integers are indispensable in these processes. Whether balancing a checkbook, cooking with precise measurements, or planning a budget, we rely on them to navigate these daily tasks with accuracy.
- Addition and Subtraction: Consider simple transactions, like buying groceries. You start with a certain amount of money (an integer), and as you purchase items, you subtract their prices (also integers). The remaining balance is determined by these integer operations.
- Multiplication and Division: Multiplication involving integers can illustrate concepts such as area in geometry—think of calculating the area of a rectangle, where both length and width are integers. Division, on the other hand, can help in distributing resources evenly, like dividing a pizza into equal slices.
These operations form the backbone of more complex mathematical problems and are crucial for developing problem-solving skills. Mastery of integers ensures that individuals can handle everyday calculations with confidence and precision.
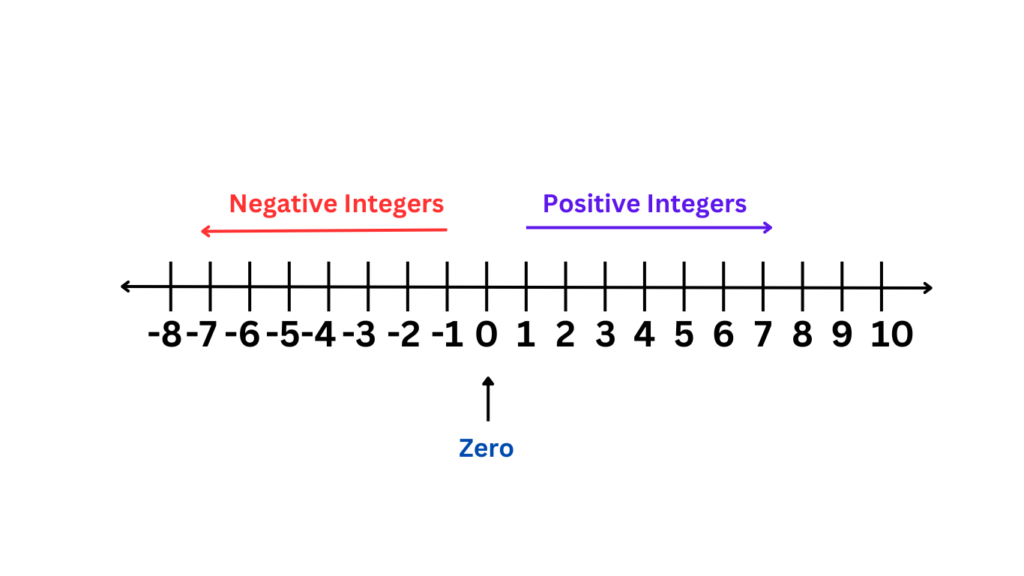
Number Line Representation
The number line is a powerful tool that brings integers to life through visual representation. Imagine a straight line stretching infinitely in both directions. At the center, we have zero. To the right of zero, we plot positive integers (1, 2, 3, …), and to the left, we place negative integers (-1, -2, -3, …).
- Understanding Magnitude: This visual layout helps us quickly grasp the relative sizes of numbers. For instance, it’s immediately apparent that +3 is greater than -2. The number line makes abstract concepts tangible, aiding in the comprehension of operations involving negative numbers.
- Direction and Distance: The number line also teaches us about direction and distance. Moving to the right signifies an increase while moving to the left indicates a decrease. This is particularly useful in real-world contexts such as temperature changes, where +10°C and -5°C are more easily understood in relation to zero.
By using a number line, students and individuals can better understand the properties of integers, making it easier to perform operations and solve problems that involve these fundamental numbers.
Algebraic Expressions
Algebra might seem intimidating at first, but at its core, it heavily relies on integers. In algebra, we often work with expressions, equations, and inequalities that incorporate it to solve for unknown values.
- Solving Equations: Whether it’s a simple equation like x + 5 = 10 or a more complex one involving multiple steps, integers are central to finding the solution. Understanding how to manipulate integers within these equations is crucial for arriving at the correct answer.
- Simplifying Expressions: Algebraic expressions, which may initially appear convoluted, become more manageable once we apply operations with integers. For instance, simplifying 3x – 2x + 7 involves recognizing that 3x and -2x are integers that can be combined to simplify the expression to x + 7.
- Graphing Inequalities: Integers are also pivotal when graphing solutions to inequalities on a number line. For example, solving x involves shading the portion of the number line where integers greater than -3 reside.
Role of Integers in Mathematics
Integers serve as the foundation for many advanced mathematical concepts and operations:
- Number Theory: Integers are essential in number theory, exploring properties like divisibility, prime numbers, and modular arithmetic.
- Algebra: Integers are used in algebraic expressions, equations, and inequalities to solve for unknown variables and simplify mathematical problems.
- Geometry: Integers find applications in geometric calculations, such as measuring distances, angles, and areas in various shapes.
Application of Integers in Daily Life Scenarios
Integers are not just theoretical concepts – they have practical applications in everyday life:
- Temperature Readings: Negative integers are used to represent temperatures below zero, while positive integers denote temperatures above zero.
- Financial Transactions: Integers are used in accounting and finance to represent gains, losses, and balances in monetary transactions.
- Distance Measurements: Integers are used to measure distances in real-world scenarios, such as road signs indicating kilometers to a destination.
- Science and Engineering: Whether calculating forces in physics, determining chemical ratios, or computing computer algorithms, integers are fundamental.
- Daily Decision Making: From cooking and travel to planning and investing, the ability to accurately compute with integers enables more informed and effective decisions.
Significance in Problem-Solving
Integers provide a structured framework for problem-solving in various contexts:
- Logical Reasoning: They are used in logical puzzles and reasoning exercises to test analytical skills and critical thinking.
- Data Analysis: They are crucial in data analysis and statistics, where numerical data is categorized and analyzed for patterns and trends.
Strategies for Identifying Integers
Recognizing integers is a fundamental skill that serves as the bedrock for more advanced mathematical concepts. Whether you’re navigating through school math problems, managing finances, or just trying to understand the numbers in everyday life, quickly and accurately identifying it is crucial. Here, we delve into effective strategies for identifying these essential numbers, focusing on whole numbers and number line representation.
- Whole Numbers: When it comes to identifying integers, the first step is to understand the scope of whole numbers. Integers encompass all whole numbers, both positive and negative, as well as zero. Understanding this comprehensive set is essential because it forms the basis for identifying and working with it in any mathematical context. Whether you’re adding, subtracting, multiplying, or dividing, knowing that all these operations can involve positive numbers, negative numbers, and zero simplifies the process.
- Number Line Representation: One of the most effective ways to understand and identify integers is through their representation on a number line. This visual tool is a straightforward yet powerful method to grasp the concept of integers and their relative positions.
Practical Examples Demonstrating the Application of Integer Properties in Problem-Solving
Let’s explore how integers are used in real-world problem-solving scenarios:
Example 1: A bank account has a balance of $500. If a withdrawal of $200 is made, the new balance can be represented as 500 – 200 = 300, showcasing the use of integers in financial transactions.
Example 2: In a temperature reading, if the current temperature is -3 degrees Celsius and it decreases by 5 degrees, the new temperature can be represented as -3 – 5 = -8, demonstrating the application of integers in measuring temperature changes.
Conclusion
Through this exploration of integers, we have uncovered the fundamental role that these numbers play in mathematics and everyday life. From basic definitions to advanced applications, it forms the backbone of numerical reasoning and problem-solving.
Recap of Key Points Covered in the Article:
- We defined integers as whole numbers that can be positive, negative, or zero, and explored their properties and significance in mathematics.
- We discussed the importance of them in basic arithmetic operations, algebraic expressions, and real-world applications like temperature readings and financial transactions.
- We highlighted its role in advanced mathematical concepts such as number theory, algebra, and geometry, showcasing their versatility and applicability.
- We provided strategies for recognizing them and practicing identification skills through exercises and examples.
- We demonstrated the practical application of its properties in problem-solving scenarios, emphasizing the relevance of integers in various contexts.
As you continue your mathematical journey, remember that they are not just numbers – they are powerful tools that can unlock a whole new world of math for you to explore and conquer.
Ways to Keep Exploring:
- Engage in number line activities to visualize them and their relationships.
- Challenge yourself with word problems and puzzles that involve its operations and logic.
- Explore advanced topics in number theory and algebra that delve deeper into the properties and applications of integers.
Frequently Asked Questions (FAQs)
Are there any numbers that are neither positive nor negative?
Yes, zero is the only number that is neither positive nor negative. It serves as the neutral element in arithmetic operations and plays a unique role in mathematics.
How are integers used in data analysis and statistics?
Integers are used to categorize and analyze numerical data in statistics, helping in identifying trends, patterns, and relationships within datasets.
Can integers be represented on a number line?
Yes, integers can be represented on a number line, where positive numbers are to the right of zero and negative numbers are to the left.