Unlocking the Secrets of the BODMAS Rule: 5 Simple Steps to Master Math

 

When you hear the BODMAS rule, what is the first thing that comes to your mind? Maybe a rule on how to eat your vegetables and beans, or a rule on how to play a game right? But to your surprise, it is none of them, rather it is a mathematical concept.

Introduction

Ever found yourself staring at a complex math problem, feeling a mix of confusion and frustration? You’re not alone! Many people struggle with solving mathematical expressions, especially when multiple operations are involved. The good news is, there’s a simple rule that can help you navigate through the chaos and find the right answer every time. It’s called the BODMAS rule, and in this article, we’ll unlock its secrets and guide you through five simple steps to master it.

What is the BODMAS Rule?

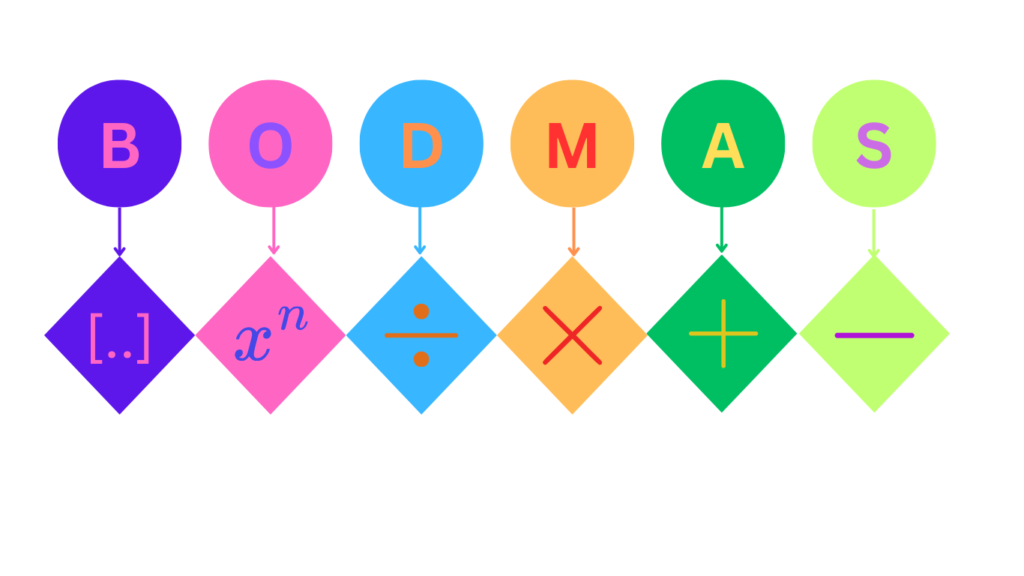
The BODMAS rule is an essential principle in mathematics that dictates the correct order of operations to follow when solving expressions involving multiple operations. BODMAS stands for:

• Brackets
• Orders (i.e., powers and roots, etc.)
• Division
• Multiplication
• Addition
• Subtraction

 

Why is the BODMAS rule important? Without it, there would be no standard way to approach mathematical problems, leading to inconsistencies and errors. The BODMAS rule ensures that everyone follows the same steps, making calculations reliable and accurate.

Breaking Down the BODMAS Rule

Understanding each component of the BODMAS rule is crucial. Let’s break it down step by step:

Brackets

Brackets are used to group parts of an expression that need to be solved first. There are different types of brackets:

• Parentheses ( ): The most common type.
• Square brackets [ ]: Often used inside parentheses.
• Curly brackets { }: Used for further grouping.

When an expression contains multiple types of brackets, solve the innermost brackets first, then move outward. The order is: solve the parentheses first, then the curly brackets, and finally the square bracket.

Example: Solve the expression 3×[2+{1+(4−2)}]

1. Innermost Brackets (Parentheses): Solve (4−2)

   • (4−2)=2
   • Expression becomes: 3×[2+{1+2}]

2. Next Brackets (Curly Brackets): Solve {1+2}

   • {1+2}=3
   • Expression becomes: 3×[2+3]

3. Outermost Brackets (Square Brackets): Solve [2+3]

   • [2+3]=5
   • Expression becomes: 3×5

4. Final Multiplication:

   • 3×5=15

So, 3×[2+{1+(4−2)}] = 15

Orders

Orders refer to exponents and roots. This step comes after brackets but before division and multiplication.

Example: In 2^3+4, solve the exponent first: 8+4=12

Division and Multiplication

These operations are performed next, and they are done from left to right, whichever comes first in the expression.

Example: In 6÷2×3, solve from left to right: 3×3=9.

Addition and Subtraction

Finally, perform addition and subtraction from left to right.

Example: In $1$, solve from left to right: 7−1=6.

How to Use the BODMAS Rule – Step-by-Step Guide

Let’s go through a detailed step-by-step guide on how to use the BODMAS rule with examples.

Step 1: Solve Brackets First

Identify and solve any expressions within brackets first.

Example: 7+(6×5)

• Solve inside the parentheses: 6×5=30
• Then add: 7+30=37

Step 2: Calculate Orders Next

Handle any exponents or roots after solving brackets.

Example: 4+2^3×2

• Solve the exponent: 2^3=8
• Then multiply: 8×2=16
• Finally add: 4+16=20

Step 3: Perform Division First

Perform these operations from left to right.

Example: 12÷3×2

• Divide first: 12÷3=4

Step 4: Perform Multiplication

Now it’s the turn of the multiplication.

• Then multiply: 4×2=8

Step 5: Complete Addition and Subtraction

Finish with addition and subtraction, moving from left to right.

Example: 10−2+5

• Subtract first: 10−2=8
• Then add: 8+5=13

Examples

1. Example 1:

   5+(2^2×3)−1
   • Brackets: 2^2×3
   • Orders: 2^2=4
   • Multiply: 4×3=12
   • Add/Subtract: 5+12−1=16

2. Example 2:

   (6+2)÷2^2
   • Brackets: 6+2=8
   • Orders: 2^2=4
   • Division: 8÷4=2

By following these steps, you can tackle any mathematical expression with confidence. Here are the steps again:

Common Mistakes and How to Avoid Them

Despite its simplicity, there are common mistakes people make when applying the BODMAS rule. Here’s how to avoid them:

Misinterpreting the Order

One frequent mistake is not following the correct sequence, especially with division and multiplication or addition and subtraction. Remember, always move from left to right for these operations.

Skipping Steps

Skipping any steps can lead to incorrect results. Ensure you solve brackets and orders before moving on to other operations.

Practice Problems

To master the BODMAS rule, practice is key. Here are a few problems to try:

1. (3+2)×5
2. 6÷2×(1+2)
3. 10+4^2−3

Solutions:

1. (3+2)×5=5×5=25
2. 6÷2×(1+2)=6÷2×3=3×3=9
3. 10+4^2−3=10+16−3=26−3=23

Benefits of Mastering the BODMAS Rule

Understanding and applying the BODMAS rule has several advantages:

Accuracy in Calculations

By following a structured approach, you ensure your calculations are accurate, reducing the risk of errors.

Confidence in Math Skills

Mastering the BODMAS rule can boost your confidence when tackling math problems, whether in school, work, or daily life.

Real-World Applications

The BODMAS rule is not just for the classroom. It’s used in various real-world scenarios, such as:

• Finance: Calculating interest, budgeting, and financial planning.
• Engineering: Designing structures, and systems, and solving technical problems.
• Computer Programming: Writing code that involves mathematical calculations.

Conclusion

The BODMAS rule is a fundamental concept that simplifies complex mathematical expressions, ensuring everyone solves them correctly and consistently. By mastering the five steps outlined in this article, you’ll enhance your math skills, boost your confidence, and be better prepared for real-world applications.

Remember, practice makes perfect, so keep working on those math problems and watch your skills grow! If you have any questions or examples you’d like to share, feel free to leave a comment below.

Frequently Asked Questions (FAQs)

Why is the BODMAS rule important?

The BODMAS rule is essential because it provides a standard method for solving mathematical expressions, ensuring consistency and accuracy in calculations.

Are there any variations of the BODMAS rule in other countries?

Yes, in some regions, PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) is used, which follows the same order of operations with a different acronym.

Can I always use a calculator to apply the BODMAS rule?

While calculators follow the BODMAS rule automatically, understanding the rule helps verify and comprehend the steps involved in the calculation.

What should I do if I make a mistake using the BODMAS rule?

If you make a mistake, revisit each step carefully to identify where you went wrong. Practice regularly to improve your accuracy and understanding.