Imagine a world without crossing paths, where lines travel endlessly side by side, never meeting, always equidistant. This is the mesmerizing realm of parallel lines. These geometric wonders are not just abstract concepts in mathematics; they play a crucial role in our daily lives, from the roads we drive on to the art that captivates us. In this article, we will explore what are parallel lines are, their properties, real-world applications, how to draw them, and what transversals do to parallel lines. Let’s dive into the captivating world of parallel lines and discover their significance in our lives.
What are Parallel Lines?
So, what are parallel lines in the technical sense? In geometry, parallel lines are defined as two straight lines that lie on the same flat surface (like a piece of paper) and never intersect, no matter how far you extend them in either direction. They remain equidistant from each other at all points. This property makes them unique and important in various fields, from mathematics to architecture.
Here’s a helpful analogy: Imagine two highways running side-by-side. No matter how long you drive on them, they’ll never touch. That’s the essence of parallel lines – they maintain a constant distance and never converge, even if you travel for miles (or color for hours!).
To solidify your understanding, let’s take a look at a visual aid:
See how line A and line B never touch, even though they extend infinitely in both directions? That’s the beauty of parallel lines – a constant, unchanging distance between them.
Similarly, in geometric notation, parallel lines are often denoted by the symbol “||”. For instance, if line A is parallel to line B, we write it as A || B. This simple notation helps convey the relationship between the lines clearly and concisely.
Properties of Parallel Lines
Now that you know the basics of what are parallel lines, let’s delve deeper into their properties. These properties act like special clues that help us identify what are parallel lines quickly. Here are the key ones to remember:
- Equidistant Nature: One of the defining features of parallel lines is that they are always equidistant from each other. This means the distance between the two lines remains constant at every point along their length. This property is crucial in ensuring consistency and precision in various applications, such as construction and design.
- No Intersection Points: Parallel lines never intersect. No matter how far they are extended, they will never cross each other. This non-intersecting property distinguishes them from other types of lines like perpendicular lines, that may intersect at one or more points.
- Same Slope in Coordinate Geometry: In the context of coordinate geometry, parallel lines have the same slope. The slope of a line measures its steepness, and for parallel lines, this value is identical. For example, if one line has a slope of ‘m’, any line parallel to it will also have a slope of ‘m’. This characteristic helps in identifying and working with parallel lines on a graph.
Parallel Lines and Transversals
Now, that we have converted all the basics of what are parallel lines, things get a bit more interesting. Imagine you have two parallel lines running happily along, and then – BAM! – a third line cuts straight across them. This brave line, the party crasher (not really, it serves a purpose!), is called a transversal.
When a transversal cuts across parallel lines, it creates special angles at the points of intersection. These angles have cool names like opposite, corresponding, alternate interior, alternate exterior, and co-interior angles. Don’t worry, we won’t bombard you with all the technical details, but here’s the gist: these special angle pairs have a unique relationship that helps us identify parallel lines.
For instance, vertically opposite angles are formed by the transversal and they will always be equal. In the picture below, line Z runs across the two parallel lines A and B and has formed vertically opposite angles and here, ∠ m = ∠ n, ∠o = ∠ p, ∠ q = ∠ c, and ∠ x = ∠ y.
Likewise, corresponding angles (think of them as angles that “correspond” to each other across the transversal) are always equal when dealing with parallel lines. It’s like a secret handshake between the angles – if they match up perfectly, it’s a strong hint that the lines they’re on might be parallel. Here in the picture below, ∠ m = ∠ x, ∠ o = ∠ q, ∠ p = ∠ c, and ∠ n = ∠ y.
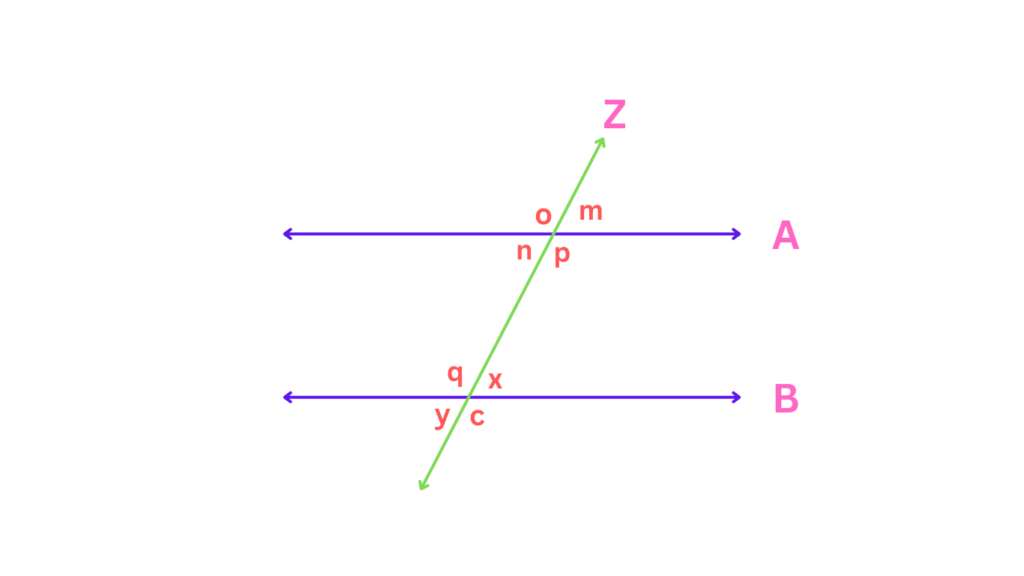
Similarly, alternate interior angles are pairs of angles formed on opposite sides of the transversal but inside the parallel lines. These angles are congruent, meaning they are equal. For example, in the picture above, ∠ n = ∠ x, and ∠ p = ∠ q.
On the other hand, alternate exterior angles are similar to alternate interior angles but are located outside the parallel lines. These angles are also equal. When a transversal crosses parallel lines, alternate exterior angles provide a mirror image of each other across the transversal, i.e. in the picture above, ∠ m = ∠ y, and ∠ o = ∠ c.
Finally, co-interior angles, also known as consecutive interior angles, are pairs of angles on the same side of the transversal and inside the parallel lines. Unlike the other pairs, co-interior angles are supplementary, meaning their measures add up to 180 degrees. This relationship is critical for solving various geometric problems and proofs. For example, in the picture above, ∠ p + ∠ x = 180 degrees, and ∠ n + ∠ q = 180 degrees.
How to Draw Parallel Lines
Now that we have learned everything about parallel lines from what are parallel lines to angles formed in parallel lines because of the transversals, it is time for some drawing. Drawing parallel lines accurately is an essential skill in geometry, art, and various practical applications. Here’s a step-by-step guide to drawing parallel lines:
Using a Ruler and Set Square:
- Draw the First Line: Start by drawing a straight line using a ruler. Ensure it’s as long as you need for your specific task.
- Position the Set Square: Place the set square so that one of its edges aligns perfectly with the first line. The set square has a right angle, which helps in maintaining the correct orientation.
- Draw the Second Line: Hold the set square steady and draw the second line along the other edge of the set square. This second line will be parallel to the first.
Using a Compass:
- Draw the First Line: Begin by drawing a straight line with a ruler.
- Set the Compass Width: Adjust the compass to a specific width, which will be the distance between the two parallel lines.
- Mark Arcs Above and Below: Place the compass point on one end of the first line and draw arcs above and below the line.
- Draw the Second Line: Move the compass to the other end of the line and draw another set of arcs. Connect these arcs to form the second parallel line.
These methods ensure accuracy and consistency, making it easier to work with parallel lines in various projects.
Real-World Applications of Parallel Lines
Does only learning what are parallel lines without knowing their use in the real world make any sense? It’s like only gaining half knowledge and we know that ‘Half Knowledge is dangerous’ so, let us also dive into the real-world applications of parallel lines. Parallel lines are not just confined to the pages of geometry textbooks; they have numerous practical applications in our daily lives.
- Architecture and Construction: In architecture, parallel lines are used to design buildings and structures that are both aesthetically pleasing and structurally sound. Floor plans, walls, and beams often rely on parallel lines to ensure stability and balance. For example, the walls of a building are typically parallel to ensure that the structure is symmetrical and well-balanced.
- Urban Planning and Road Design: Urban planners use parallel lines to create organized and efficient road systems. Streets and avenues in many cities are laid out in a grid pattern, with parallel lines ensuring consistent spacing and ease of navigation. This design helps manage traffic flow and improves safety at intersections.
- Art and Design: Artists and designers often use parallel lines to create balance and symmetry in their work. Whether it’s a painting, a sculpture, or a graphic design project, parallel lines can enhance visual appeal and structure. For instance, the use of parallel lines in perspective drawing helps create the illusion of depth and distance.
Conclusion
So, there you have it! You’ve conquered the world of parallel lines – from what are parallel lines and properties to learning how to draw them. Parallel lines are a fundamental concept in geometry, playing a crucial role in both theoretical and practical applications. Understanding parallel lines enriches our appreciation of the structures and designs around us. Next time you look at a road, a building, or a piece of art, take a moment to appreciate the magic of parallel lines. Keep exploring the geometric world around you, and you’ll find that parallel lines are indeed fascinating and essential.
Frequently Asked Questions (FAQs)
What Are Parallel Lines in Geometry?
Parallel lines are two lines in the same plane that never intersect and remain equidistant from each other at all points. They have the same slope in coordinate geometry and are denoted by the symbol “||”.
How Do You Identify Parallel Lines on a Graph?
On a graph, parallel lines can be identified by their equal slopes. If two lines have the same slope but different y-intercepts, they are parallel and will never intersect.
How Are Parallel Lines Different from Perpendicular Lines?
Parallel lines never intersect and remain equidistant, while perpendicular lines intersect at a right angle (90 degrees). This difference is crucial in understanding geometric relationships and solving problems involving lines.
One Comment
Comments are closed.