Ever doodled a cool four-sided shape but struggled to remember its name? Fear not, fellow shape enthusiasts. Today, we’re diving headfirst into the captivating world of quadrilaterals.
What are quadrilaterals, you ask? Well, they’re the champions of the four-sided shape game. Imagine a box without a top, or a delicious pizza box waiting to be filled with cheesy goodness – that’s a quadrilateral. But there’s so much more to these shapes than meets the eye. Buckle up and get ready to explore their fascinating properties and diverse family members.
What are Quadrilaterals?
So, what are quadrilaterals? Quadrilaterals are four-sided polygons with four angles. The word “quadrilateral” comes from the Latin words “quadri,” meaning four, and “latus,” meaning side. These shapes are fundamental in geometry and can be found everywhere in our daily lives, from the books we read to the buildings we live in. Think of a flat cereal box – that’s a perfect example of a quadrilateral.
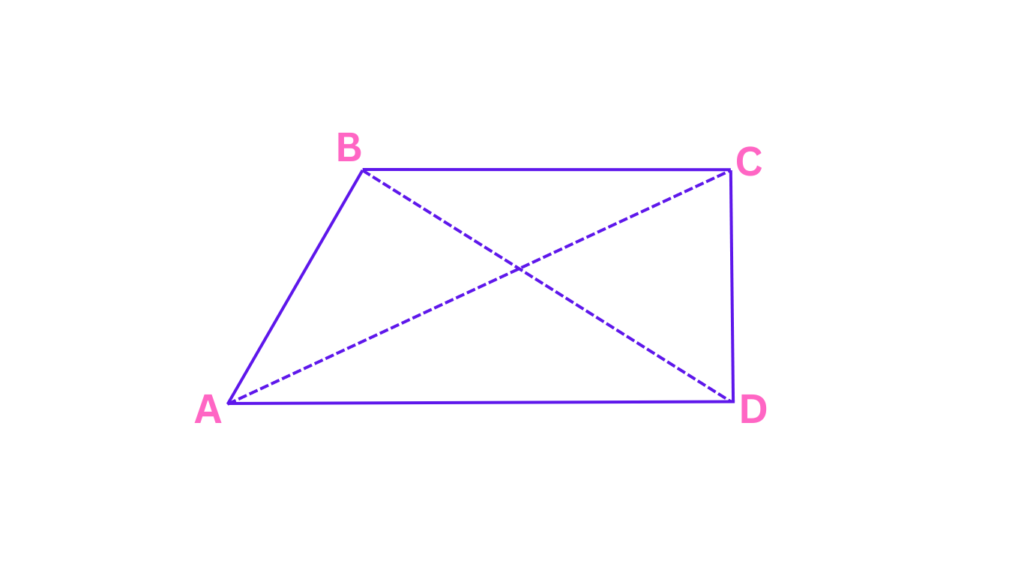
Properties of Quadrilaterals
Now that we know what quadrilaterals are, let’s delve deeper into their defining characteristics:
- The 4-Side Squad: The first thing that unites all quadrilaterals, regardless of type, is – you guessed it – their four sides. They’re the shape squad with four members, forming a closed loop.
- Angles Aplenty: Next up, we have angles. Every quadrilateral boasts four angles, just like the four corners of a room. What are quadrilaterals without their angles? They wouldn’t be able to define their shape. Interestingly, the sum of all these angles in any quadrilateral always adds up to 360 degrees.
- Diagonals: Diagonals add another layer of intrigue to quadrilaterals. These are line segments that act like brave explorers, venturing from one corner of the shape directly to the opposite corner. Not all quadrilaterals have special properties related to diagonals, but we’ll encounter some fascinating exceptions later on in our journey.
These simple properties make quadrilaterals unique and distinct from other polygons.
Types of Quadrilaterals
Now that we’ve covered the basics of what are quadrilaterals, let’s dive into the different types. Each type has its own set of properties and characteristics.
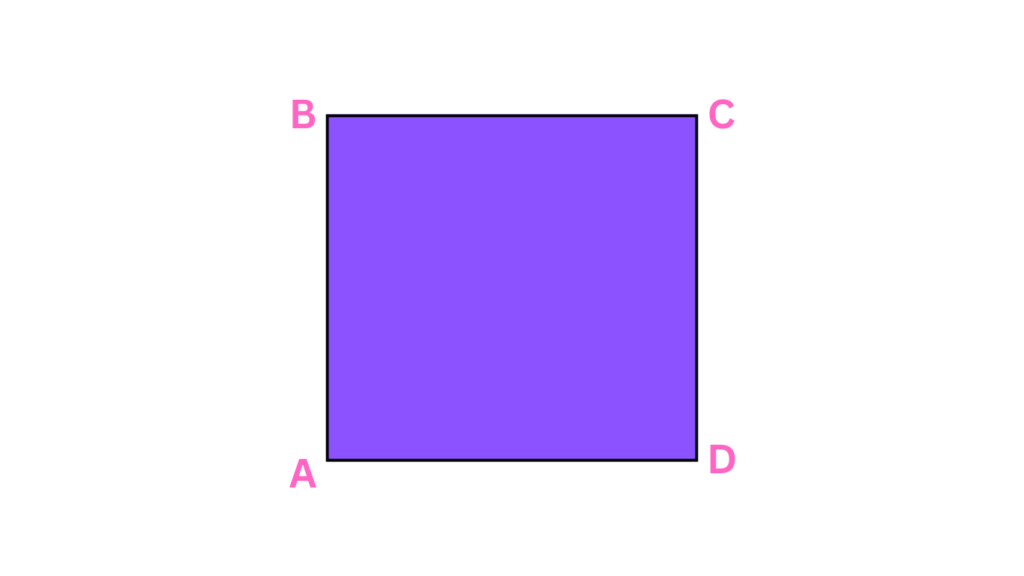
Squares
Ah, the perfectionists of the group! Squares are like the overachievers of the quadrilateral family. They have four sides that are all equal in length, and to top it off, all four angles are perfect right angles (think of a Rubik’s Cube – every side and angle is meticulously aligned).
- Properties: All sides are equal, all angles are 90 degrees, and diagonals bisect each other at right angles and are equal in length.
- Real-Life Examples: Chessboards and tiles are often in the shape of squares.
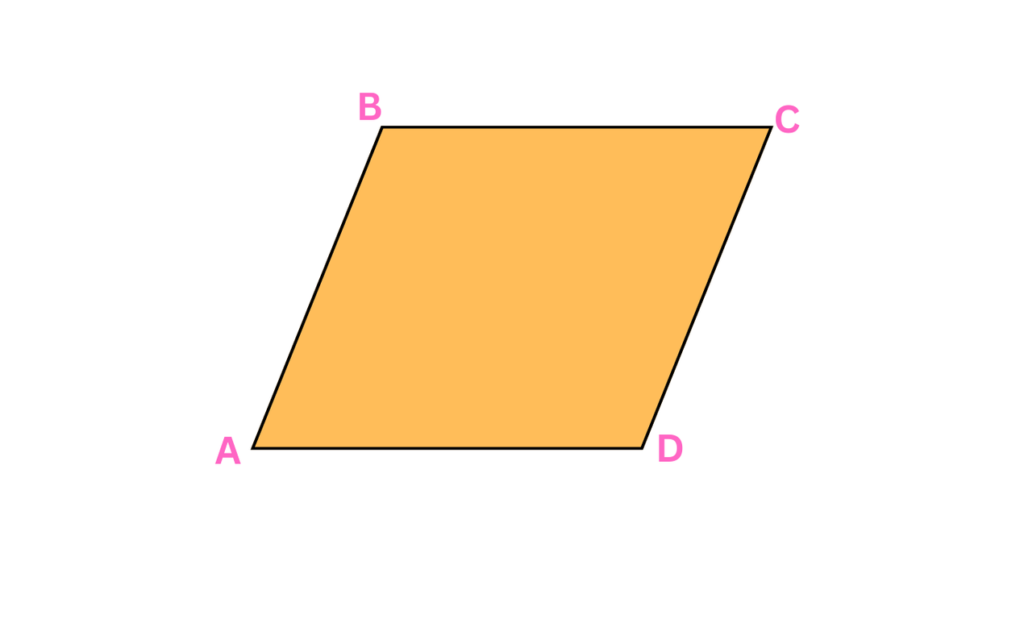
Parallelograms
Parallelograms are a type of quadrilateral where opposite sides are parallel and equal in length. The opposite angles are also equal.
- Properties: Opposite sides are parallel and equal, opposite angles are equal, and diagonals bisect each other.
- Examples: Common examples include rectangles and rhombuses.
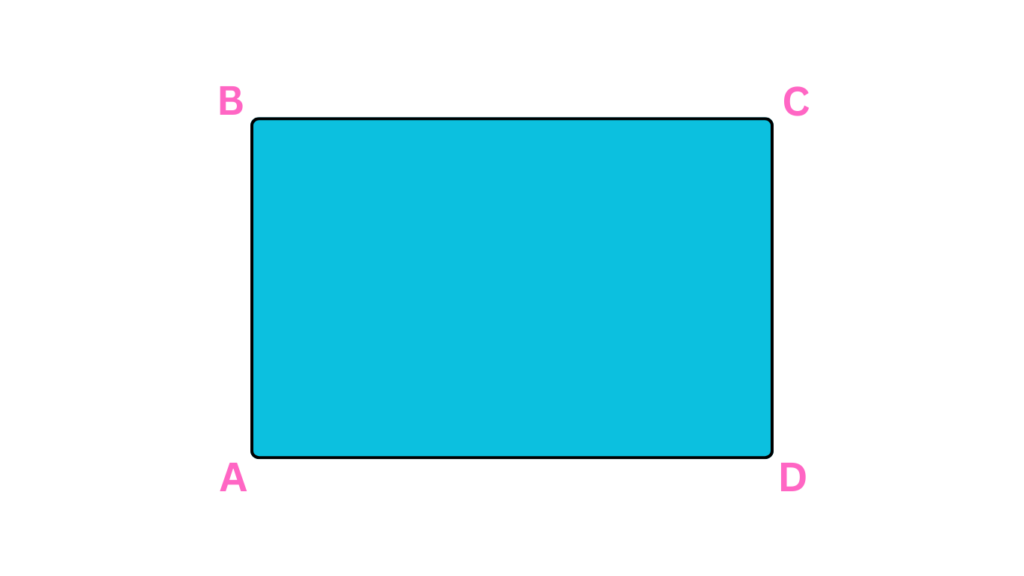
Rectangles
Rectangles are parallelograms with four right angles. They are squares’ slightly more relaxed cousins. They share the property of having opposite sides that are equal in length.
- Properties: All angles are 90 degrees, opposite sides are equal and parallel, and diagonals are equal in length.
- Real-Life Examples: Think of your smartphone, a door, or a book – all rectangles!
Rhombuses
Ever seen a square that’s been squished a little? That’s a rhombus! They have four sides that are all equal in length, just like squares, but their angles aren’t all right angles.
- Properties: All sides are equal, opposite angles are equal, and diagonals bisect each other at right angles.
- Real-Life Examples: A diamond shape in playing cards is a perfect example of a rhombus.
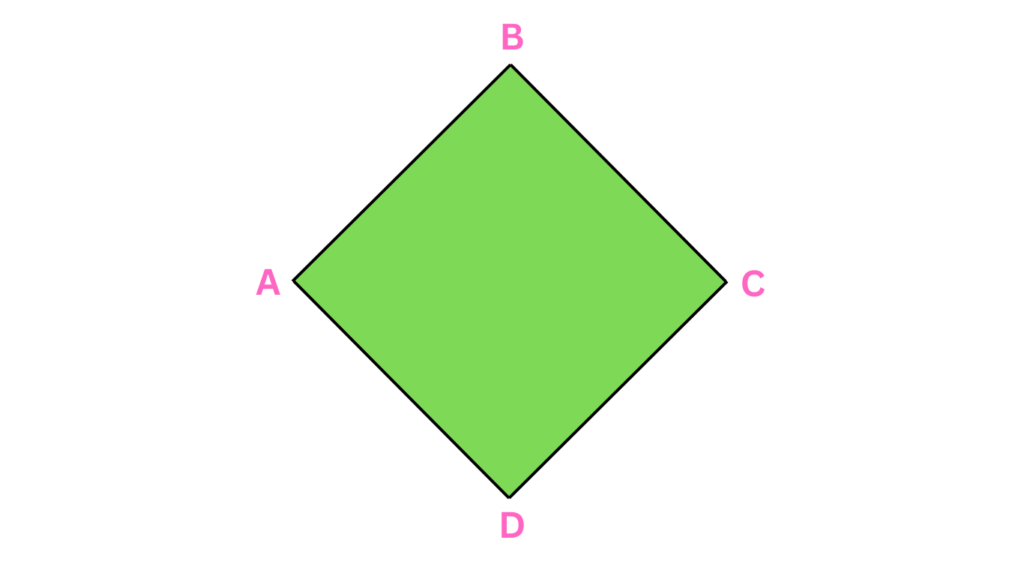
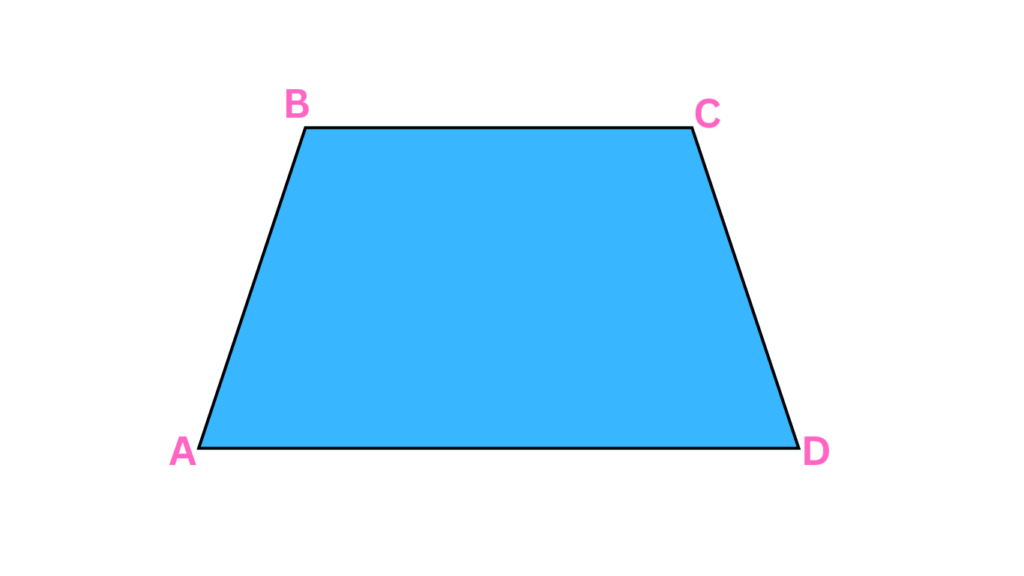
Trapezoids (Trapezia)
Trapezoids are quadrilaterals with at least one pair of parallel sides.
- Properties: One pair of opposite sides is parallel, and the non-parallel sides are called legs.
- Real-Life Examples: The shape of a typical table or a bridge cross-section can often be trapezoidal.
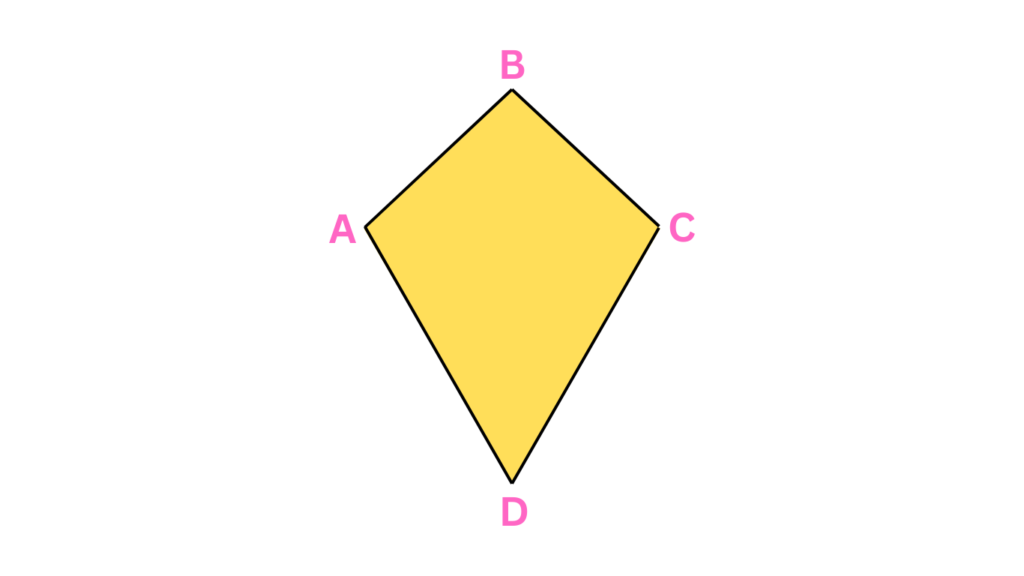
Kites
Kites are quadrilaterals with two pairs of adjacent sides that are equal. These playful members of the quadrilateral family are a special type of trapezoid.
- Properties: Two pairs of adjacent sides are equal, one pair of opposite angles is equal, and diagonals intersect at right angles.
- Real-Life Examples: As the name suggests, traditional kite shapes are a perfect example of this type of quadrilateral.
Classification of Quadrilaterals
As we’ve explored, what are quadrilaterals but a diverse group of shapes? But how do we keep track of them all? Mathematicians have developed a classification system to categorize quadrilaterals based on their properties. Here’s a peek:
- Convex vs. Concave Quadrilaterals: Convex quadrilaterals have all their interior angles pointing outwards and always have interior angles less than 180 degrees. Imagine a bouncy castle – its inflatable walls form a convex quadrilateral. On the other hand, concave quadrilaterals have at least one angle that curves inwards, like a flattened cardboard box, i.e. one interior angle will always be more than 180 degrees.
- Simple vs. Complex Quadrilaterals: Simple quadrilaterals, like squares and rectangles, have no intersecting sides (except at the corners). Complex quadrilaterals, like some types of self-intersecting stars, might have sides that cross each other.
Real-Life Applications of Quadrilaterals
What are quadrilaterals good for in the real world? You might be surprised at how often you encounter them. From the foundations of our homes (rectangles for walls) to the furniture we use (squares for tabletops) to the very signs that guide us, quadrilaterals play a vital role in our everyday lives.
Architecture and Engineering
Quadrilaterals are fundamental in the design and construction of buildings and structures.
- Buildings: Many buildings and rooms are designed using rectangular shapes for stability and ease of construction.
- Bridges: Trapezoidal shapes are common in bridge designs for strength and support.
Art and Design
Artists and designers frequently use quadrilaterals in their work.
- Graphic Design: Rectangles and squares are commonly used in layout design and framing elements.
- Patterns: Rhombuses and kites often appear in artistic patterns and tiling.
Everyday Objects
Quadrilaterals are all around us in everyday objects.
- Books and Screens: Most books, screens, and monitors are rectangular.
- Tables and Windows: Tables and windows often come in rectangular or trapezoidal shapes.
Conclusion
In summary, understanding what are quadrilaterals opens up a fascinating world of shapes and their applications. Quadrilaterals are four-sided polygons with diverse types and properties, playing vital roles in geometry and real life. From the buildings we live into the art we admire, quadrilaterals are everywhere. By recognizing their properties and applications, we can appreciate the magic behind these shapes. So next time you see a book, a table, or a bridge, remember – it’s all about quadrilaterals! Feel free to share your thoughts, ask questions, or explore more about these incredible shapes in the comments below.
Frequently Asked Questions (FAQs)
What are quadrilaterals?
Quadrilaterals are four-sided polygons with four angles. They include shapes like squares, rectangles, and trapezoids.
How many types of quadrilaterals are there?
There are several types of quadrilaterals, including parallelograms, rectangles, rhombuses, squares, trapezoids, and kites.
What is the difference between a parallelogram and a trapezoid?
A parallelogram has two pairs of parallel sides, while a trapezoid has only one pair of parallel sides.
Are all rectangles squares?
No, not all rectangles are squares. A square is a special type of rectangle where all sides are equal.
What are the properties of a rhombus?
A rhombus has all sides equal, opposite angles equal, and diagonals that bisect each other at right angles.
How can I identify a kite among other quadrilaterals?
A kite has two pairs of adjacent sides that are equal, and its diagonals intersect at right angles.
Why are quadrilaterals important in real life?
Quadrilaterals are important in various fields such as architecture, engineering, art, and design. They provide structural stability and aesthetic appeal.
One Comment
Comments are closed.