Ever wondered how a simple geometric shape like a cube plays a crucial role in both math and real life? This article will dive deep into the fascinating world of what is a cube, revealing its secrets, uses, and formulas. Whether you’re a student, a teacher, or just a curious mind, understanding what a cube is will provide valuable insights into geometry and beyond.
What Is a Cube?
So, what is a cube? A cube is a three-dimensional geometric shape with six equal square faces, twelve edges, and eight vertices. It’s also known as a regular hexahedron and is one of the five Platonic solids, which are convex polyhedra with faces that are congruent regular polygons. In simpler terms, all the faces of a cube are squares, and they meet at right angles.
When you think about what is a cube, imagine a standard dice or a Rubik’s Cube. These are perfect examples of cubes we encounter in our daily lives. Each face of the cube is identical, and each edge is of the same length, making it a symmetrical and aesthetically pleasing shape.
Historical Background
The concept of a cube has been around for centuries. The ancient Greeks, particularly the mathematician Plato, studied and wrote extensively about the cube. Plato categorized the cube as one of the five Platonic solids, which he believed were the building blocks of the universe.
In ancient architecture, cubes have been used in various designs due to their structural stability and simplicity. For instance, many ancient temples and buildings incorporate cube-like structures, showcasing the timeless appeal of this geometric shape.
Characteristics of a Cube
Now that we know what is a cube, let’s dive deeper and explore its defining characteristics:
- Six Faces: The defining characteristic of a cube is its six faces. Each of these faces is a perfect square, meaning all four sides of each face have the same length. Imagine a die – each side you see is a square, making it a perfect example of a cube.
- Twelve Edges and Eight Vertices: But a cube isn’t just about faces. These squares meet each other at line segments called edges. There are a total of 12 edges in a cube, with each edge connecting exactly two faces. Additionally, the points where three edges meet are called vertices. If you count the corners of a Rubik’s Cube, you’ll find exactly 8 vertices.
- Equal Angles: Finally, when you measure each internal angle between the faces of the cube it is 90 degrees, making it a right-angled shape.
These properties make the cube a unique and easily recognizable shape in geometry.
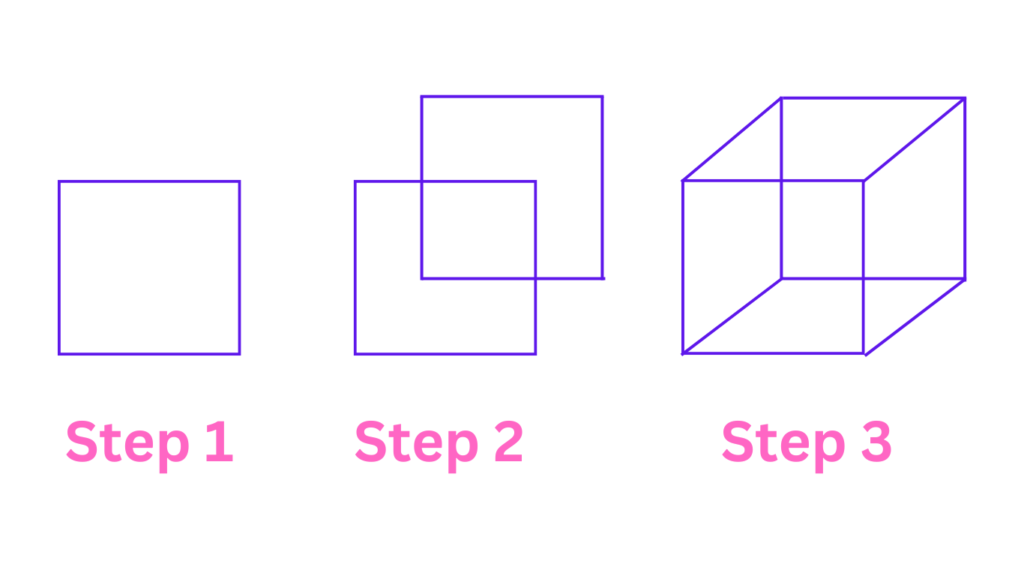
How to Draw and Imagine a Cube
Now that you’re armed with knowledge about cubes, let’s get creative Here are some ways to visualize and draw a cube:
- Start with a Square: Draw a basic square on your paper. This will represent one of the faces of your cube.
- Creating Depth: To add a 3D feel, draw another square behind the first one, slightly offset to the right and upwards. Imagine this second square as if you’re looking at the top face of the cube from a slightly angled view.
- Connecting the Faces: Now comes the magic! Using light lines, connect the corresponding corners of the two squares you drew. These lines will represent the edges of the cube.
- Completing the Cube: Extend the top and bottom edges of the back square slightly forward to meet the front square. This creates the illusion of depth and completes the basic drawing of a cube.
Formulas Related to a Cube
One of the critical aspects of understanding what is a cube involves learning the various mathematical formulas associated with it. Here are the essential formulas:
- Volume of a Cube
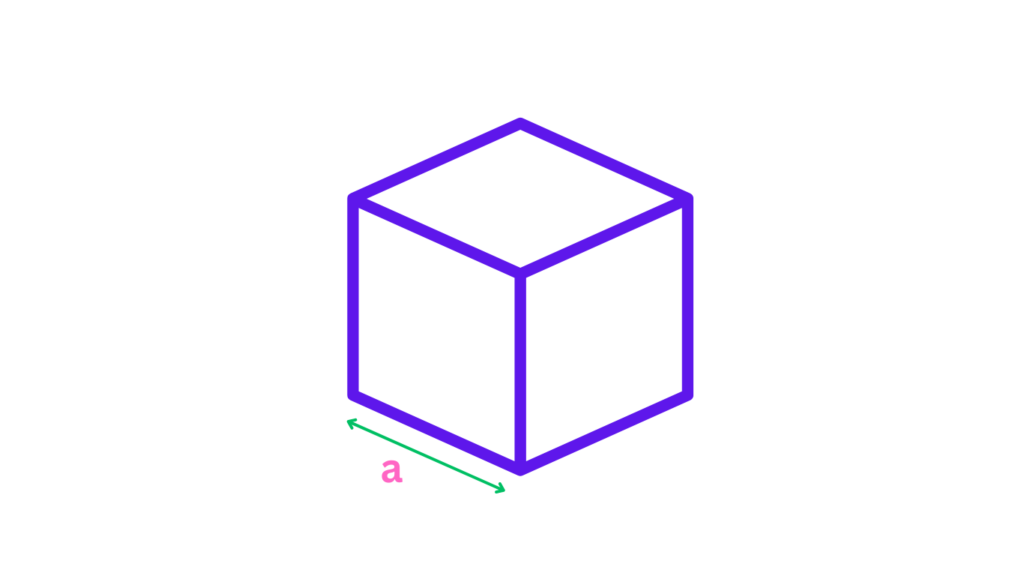
Formula: V = a³
Explanation: The volume is calculated by cubing the length of one edge. If each edge of the cube is ‘a’ units long, then the volume is ‘a’ multiplied by itself twice.
Example: If the edge length (a) is 3 units, then the volume (V) = 3³ = 27 cubic units.
- Surface Area of a Cube
Formula: SA = 6a²
Explanation: The surface area is the total area of all six faces. Since each face is a square, and the area of a square is ‘a²’, you multiply by six to get the surface area.
Example: If the edge length (a) is 4 units, then the surface area (SA) = 6 * 4² = 6 * 16 = 96 square units.
- The diagonal of a Face
Formula: d = a√2
Explanation: This formula calculates the diagonal of one face of the cube. Since the face is a square, the diagonal can be found using the Pythagorean theorem.
Example: If the edge length (a) is 2 units, then the diagonal (d) = 2√2 ≈ 2.828 units.
- Space Diagonal of a Cube
Formula: D = a√3
Explanation: This is the diagonal that cuts through the center of the cube from one vertex to the opposite vertex. It can be calculated using the three-dimensional version of the Pythagorean theorem.
Example: If the edge length (a) is 1 unit, then the space diagonal (D) = 1√3 ≈ 1.732 units.
Real-Life Applications of Cubes
Knowing what is a cube extends beyond theoretical knowledge. Cubes have practical applications in various fields:
- Architecture and Building Design
Cubes are a fundamental shape in architecture due to their simplicity and structural integrity. Many buildings and structures use cube-like designs for their aesthetic appeal and practicality. For example, modern architecture often features minimalist cube shapes to create clean, functional spaces.
- Packing and Storage Solutions
Cubes are efficient for packing and storage because they maximize space usage. When you pack cubes, there’s minimal wasted space between them, making them ideal for shipping and storage industries. This efficiency is why boxes and crates are often cube-shaped.
- Rubik’s Cube and Puzzles
The Rubik’s Cube, one of the most popular puzzles globally, is a cube. This 3D combination puzzle has fascinated and challenged people for decades. Understanding what a cube is can give you a better appreciation of the complexity and design of such puzzles.
- Technology and Computing
In technology, cubes are used in data storage and representation. For example, data cubes are used in databases to represent multidimensional data efficiently. This helps in organizing and analyzing large amounts of information quickly and effectively.
Fun Facts and Trivia
Exploring what is a cube can lead to some interesting and fun facts:
- Cultural Significance: In various cultures, the cube symbolizes stability and balance. Its symmetrical shape represents order and harmony.
- Historical References: Ancient mathematicians, like the Greeks and Egyptians, studied cubes extensively, contributing to our modern understanding of geometry.
- Cubes in Art: Many artists use cubes in their work to explore dimensions and perspectives. For example, Cubism, an influential art movement, uses geometric shapes, including cubes, to depict objects from multiple angles.
Common Misconceptions
When learning about what is a cube, several misconceptions can arise:
- Cube vs. Square: A common mistake is confusing a cube with a square. While a square is a two-dimensional shape with four equal sides, a cube is three-dimensional with six square faces.
- Rectangular Prism vs. Cube: Another misconception is equating a cube with a rectangular prism. While both are three-dimensional, a cube has all sides equal, whereas a rectangular prism has sides that can be of different lengths.
- Volume and Surface Area Confusion: People often mix up the formulas for volume and surface area. Remember, volume is about how much space is inside the cube (V = a³), while surface area is the total area of all faces (SA = 6a²).
Conclusion
Understanding what is a cube reveals its significance in both mathematical theory and practical applications. From its geometric properties and formulas to its real-life uses and cultural significance, the cube is a powerful shape that continues to intrigue and inspire. Whether you’re solving a Rubik’s Cube or designing a building, the cube’s simple yet profound structure plays a crucial role. Embrace this timeless geometric shape and discover how it can simplify and enhance your understanding of the world around you.
By exploring the properties, formulas, and applications of cubes, we gain a deeper appreciation for this fundamental shape. So next time you see a cube, remember that there’s more to it than meets the eye. Dive into the world of cubes and unlock the amazing secrets of this powerful geometric shape.
Frequently Asked Questions (FAQs)
What is a cube in geometry?
A cube in geometry is a three-dimensional shape with six equal square faces, twelve edges, and eight vertices. It is a type of polyhedron with all faces congruent.
How do you calculate the volume of a cube?
To calculate the volume of a cube, use the formula V = a³, where ‘a’ is the length of an edge. Multiply the edge length by itself twice to get the volume.
What are the properties of a cube?
A cube has six equal square faces, twelve equal edges, and eight vertices. The internal angles between faces are all 90 degrees.
How is a cube different from a rectangular prism?
A cube has all sides of equal length, while a rectangular prism can have sides of different lengths. A rectangular prism is a more general form of a cuboid.
Why are cubes important in real life?
Cubes are important due to their structural stability and efficiency in packing and storage. They are also used in technology, puzzles, and architecture, making them versatile and practical shapes.