Ever wondered what the fancy term is for a box? Look no further than the cuboid! These might sound complicated, but what is a cuboid? Cuboids are actually the 3D rockstars behind your favorite boxes, buildings, and even your phone. They might not be as flashy as pyramids or spheres, but cuboids are the unsung heroes of the 3D world.
In this guide, we’ll be diving deep into the world of cuboids. We’ll answer the question of what is a cuboid in a way that’s clear, concise, and (dare we say) fun. So, buckle up and get ready to conquer 3D with your newfound cuboid knowledge.
What Is a Cuboid?
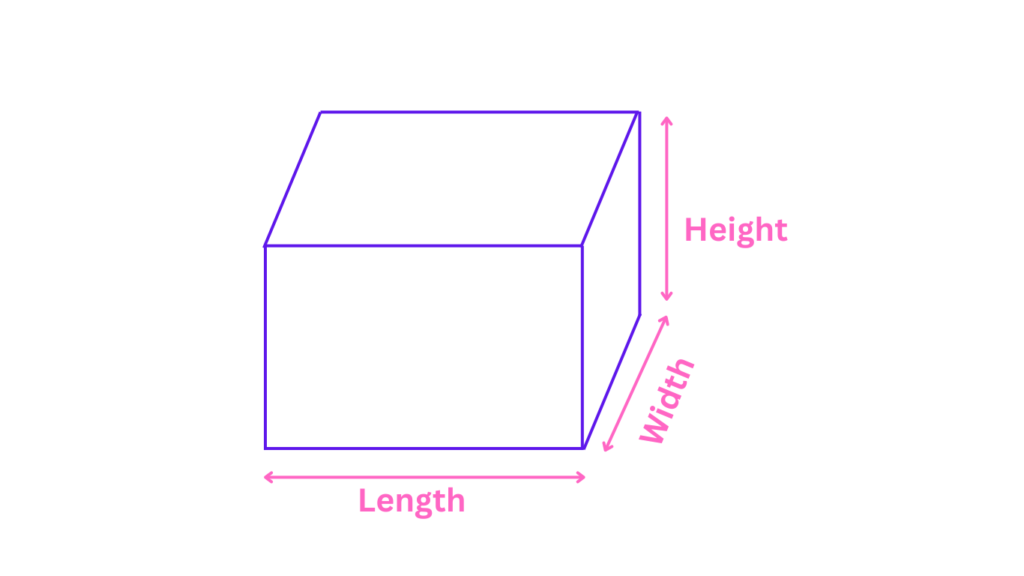
So, what is a cuboid? A cuboid is a three-dimensional geometric shape with six rectangular faces, twelve edges, and eight vertices. Unlike cubes, which have all sides equal, a cuboid’s faces can have different lengths and widths. In simple terms, think of a cuboid as a stretched or elongated cube.
When we talk about what is a cuboid, we’re referring to a shape that is everywhere in our daily lives. Examples include books, bricks, cereal boxes, and even some pieces of furniture. Each face of a cuboid is a rectangle, and opposite faces are equal in size. This characteristic makes cuboids a versatile and essential shape in both mathematics and real-world applications.
Historical Background
The concept of a cuboid has been around for centuries. The ancient Egyptians, known for their architectural prowess, used cuboids extensively in construction. The design of the pyramids, while primarily triangular, incorporated cuboid shapes in their base structures and inner chambers.
Greek mathematicians, including Euclid, studied cuboids and other three-dimensional shapes extensively. Euclid’s work in “Elements” laid the foundation for understanding what is a cuboid and its properties. His axioms and theorems on shapes have influenced mathematical studies for centuries.
In modern architecture, cuboids remain a fundamental shape. The simple, rectangular design of many buildings, from skyscrapers to residential homes, showcases the enduring relevance of the cuboid. This shape provides structural stability and maximizes usable space, making it a popular choice in construction.
Characteristics of a Cuboid
Understanding what is a cuboid involves examining its fundamental characteristics:
- Six Faces: Each face is a rectangle, and opposite faces are equal in size.
- Twelve Edges: The edges are the lines where two faces meet. All edges are straight and can have different lengths.
- Eight Vertices: These are the corners where three edges converge.
- Right Angles: Each internal angle between faces is 90 degrees, making it a right-angled shape.
These properties distinguish cuboids from other three-dimensional shapes. For instance, while a cube is a special type of cuboid with all equal sides, a general cuboid has varying lengths, widths, and heights.
Cuboids vs. Cubes: Knowing the Difference
Cuboids have a close cousin, the cube. They’re both 3D shapes with six faces, but there’s a key difference that helps us understand what is a cuboid and how it’s different from a cube.
In a cube, all six faces are squares (same size!). Imagine a Rubik’s cube – each side is a perfectly identical square. Cuboids, on the other hand, can have different-sized rectangular faces. So, while a cube is a very specific type of cuboid (all faces are squares), not all cuboids are cubes.
Formulas Related to a Cuboid
One of the critical aspects of understanding what is a cuboid involves learning the various mathematical formulas associated with it. Here are the essential formulas:
- Volume of a Cuboid
- Formula: V = l * w * h
- Explanation: The volume is calculated by multiplying the length (l), width (w), and height (h). This formula gives the amount of space inside the cuboid.
- Surface Area of a Cuboid
- Formula: SA = 2lw + 2lh + 2wh
- Explanation: The surface area is the total area of all six faces. By calculating the area of each pair of opposite faces and summing them, we get the total surface area.
- The diagonal of a Face
- Formula: d = √(l² + w²)Explanation: This formula calculates the diagonal of one rectangular face of the cuboid using the Pythagorean theorem.
- Space Diagonal of a Cuboid
- Formula: D = √(l² + w² + h²)
- Explanation: This is the diagonal that cuts through the cuboid from one vertex to the opposite vertex. It can be calculated using the three-dimensional version of the Pythagorean theorem.
Real-Life Applications of Cuboids
Knowing what is a cuboid extends beyond theoretical knowledge. Cuboids have practical applications in various fields:
- Architecture and Building Design
Cuboids are a fundamental shape in architecture due to their simplicity and structural integrity. Many buildings and structures use cuboid designs for their aesthetic appeal and practicality. For example, modern architecture often features minimalist cuboid shapes to create clean, functional spaces. The rectangular design allows for efficient space utilization and easy construction.
- Packaging and Storage Solutions
Cuboids are efficient for packaging and storage because they maximize space usage. When you pack cuboids, there’s minimal wasted space between them, making them ideal for shipping and storage industries. This efficiency is why boxes and crates are often cuboid-shaped. They stack neatly and provide stability during transportation.
- Everyday Objects
Many everyday objects are cuboid in shape. Books, bricks, cereal boxes, and electronic devices often have a cuboid design. This shape is practical for manufacturing and storage, making it a common choice for various products. Understanding what a cuboid is can help you appreciate the design and functionality of these items.
- Technology and Computing
In technology, cuboids are used in data storage and representation. For example, data structures in computing, such as arrays and matrices, often visualize data in a cuboid format. This helps in organizing and analyzing large amounts of information efficiently. Understanding what a cuboid is can give you insights into how data is structured and managed in the digital world.
Fun Facts and Trivia
Exploring what is a cuboid can lead to some interesting and fun facts:
- Cultural Significance: In various cultures, the cuboid symbolizes stability and practicality. Its symmetrical shape represents order and functionality.
- Historical References: Ancient mathematicians, like the Greeks and Egyptians, studied cuboids extensively, contributing to our modern understanding of geometry.
- Cuboids in Art: Many artists use cuboids in their work to explore dimensions and perspectives. For example, minimalist art often incorporates cuboid shapes to convey simplicity and balance.
Common Misconceptions
When learning about what is a cuboid, several misconceptions can arise:
- Rectangular Prism vs. Cuboid: One misconception is equating a cuboid with a rectangular prism. Technically, a cuboid is a rectangular prism, but the term “cuboid” is more commonly used to emphasize the rectangular faces.
- Volume and Surface Area Confusion: People often mix up the formulas for volume and surface area. Remember, volume is about how much space is inside the cuboid (V = l * w * h), while surface area is the total area of all faces (SA = 2lw + 2lh + 2wh).
Conclusion
Understanding what is a cuboid reveals its significance in both mathematical theory and practical applications. From ancient architecture to modern technology, cuboids play a crucial role in various fields. By learning about their properties, formulas, and real-life uses, we can appreciate the beauty and functionality of this essential geometric shape. So, next time you see a book, a box, or a building, take a moment to recognize the cuboid’s contribution to our world.
Frequently Asked Questions (FAQs)
What is a cuboid in geometry?
A cuboid in geometry is a three-dimensional shape with six rectangular faces, twelve edges, and eight vertices. It is a type of polyhedron where all faces are rectangles, and opposite faces are equal in size.
How do you calculate the volume of a cuboid?
To calculate the volume of a cuboid, use the formula V = l * w * h, where ‘l’ is the length, ‘w’ is the width, and ‘h’ is the height. Multiply these dimensions to get the volume.
What are the properties of a cuboid?
A cuboid has six rectangular faces, twelve edges, and eight vertices. The internal angles between faces are all 90 degrees. Opposite faces are equal in size.
How is a cuboid different from a rectangular prism?
A cuboid is a specific type of rectangular prism. While both terms are often used interchangeably, “cuboid” typically emphasizes the rectangular nature of the faces, whereas “rectangular prism” is a broader term that can refer to any prism with rectangular faces.
Why are cuboids important in real life?
Cuboids are important due to their structural stability and efficiency in packing and storage. They are used in architecture, packaging, everyday objects, and technology, making them versatile and practical shapes.