Ever feel confused by those squiggly lines and mysterious letters staring back at you from a math problem? Numbers jumbled together, strange symbols lurking in the shadows – it can all feel like a code waiting to be cracked. But fear not! They are just equations.
What is an equation you ask? It is a mathematical statement that asserts the equality of two expressions. Sound interesting right? So, let’s dive further into the magic of what is an equation in this article. It will guide you through everything you need to know about what is an equation, from the basics to advanced techniques.
What is an Equation?
Let us start with a simple definition of what is an equation. An equation is a mathematical statement that uses an equal sign (=) to declare that two expressions have the same value. Imagine a perfectly balanced scale – on each side, you have different stuff (like numbers or mysterious letters), but in the end, they balance out to be equal. That’s the essence of an equation: two expressions, seemingly different, yet holding the same weight in the grand scheme of things.
Visual Breakdown:
To truly grasp what an equation is, let’s visualize it. Take a look at this simple equation: 3x + 5 = 11. This equation has two main parts, separated by the mighty equal sign (=).
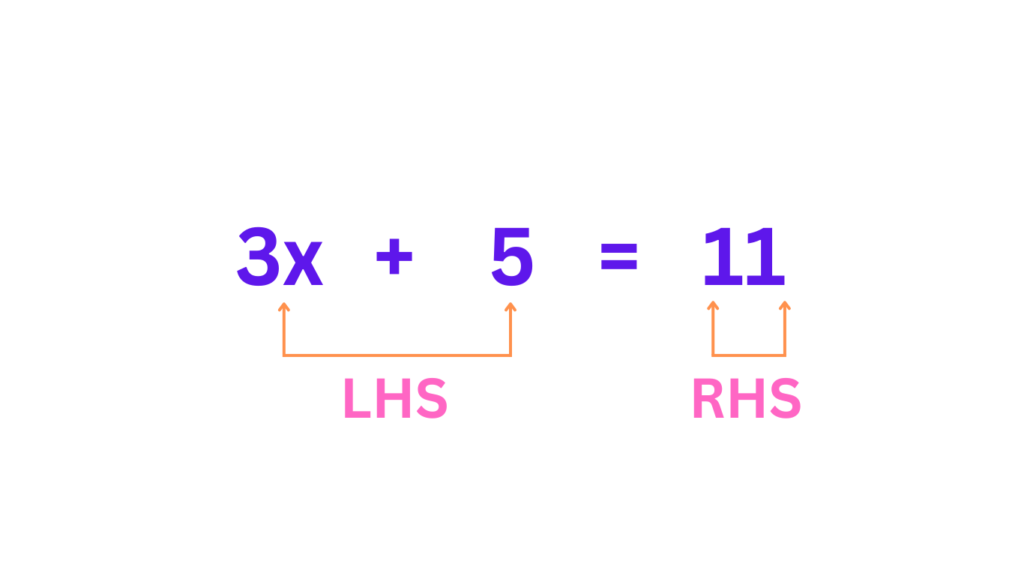
Here’s the breakdown:
- Left-Hand Side (LHS): This is everything to the left of the equal sign. In our example, it’s 3x + 5. The LHS is like one pan of the balancing scale, holding an expression that could involve numbers, variables (those mysterious letters we mentioned), or even a combination of both.
- Right-Hand Side (RHS): This is everything to the right of the equal sign. Here, it’s 11. The RHS is the other pan of the scale, holding another expression that needs to balance out with the LHS.
The key takeaway? Both the LHS and RHS, despite their potentially different appearances, must have the same value for the equation to hold true. That’s the balancing act that equations are all about.
Components of an Equation
To fully grasp what is an equation, let’s break down its components in detail. Understanding these fundamental elements is crucial for anyone looking to master equations and their applications.
Variables
Variables are symbols, typically letters, that represent unknown values in an equation. They are placeholders for numbers that we aim to discover by solving the equation. Variables can change depending on the context of the problem.
- Common Variables: The most frequently used variables are x, y, and z, though any letter can serve as a variable.
- Role in Equations: Variables allow us to generalize mathematical statements and create formulas that can be applied to different situations. For example, in the equation 2x + 3 = 7, x is the variable we need to solve for.
- Dependent and Independent Variables: In some equations, especially in functions, we distinguish between dependent variables (those whose values depend on other variables) and independent variables (those whose values are chosen freely).
Constants
Constants are fixed values that do not change within the context of a given equation. These values are known and remain the same throughout the problem-solving process.
- Numerical Constants: These are specific numbers, such as 2, 3, or -5. In the equation 2x + 3 = 7, both 2 and 3 are constants.
- Symbolic Constants: Sometimes constants are represented by symbols, like a, b, or c, especially when dealing with general forms of equations (e.g., the general form of a quadratic equation ax^2 + bx + c = 0).
- Role in Equations: Constants provide the specific numerical framework that the variables operate within. They anchor the equation, giving it structure and allowing us to solve for the variables.
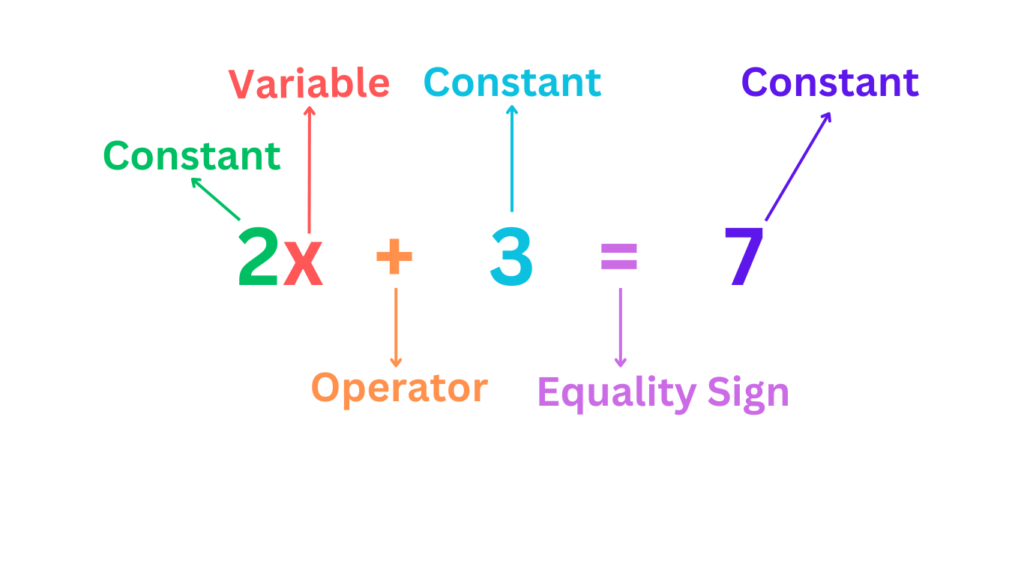
Operators
Operators are symbols that represent mathematical operations performed on the variables and constants. They dictate the actions to be taken on the numbers within the equation.
- Common Operators: The basic operators include addition (+), subtraction (-), multiplication (* or ×), and division (/ or ÷). For example, in 2x + 3 = 7, the + sign is the operator indicating addition.
- Advanced Operators: In more complex equations, you might encounter exponents (^), radicals (√), and other functions (like sine, cosine, or logarithms).
- Role in Equations: Operators define the relationships and operations that connect variables and constants. They are crucial for setting up the mathematical expressions that need to be solved.
Equality Sign
The equality sign (=) is a fundamental component of an equation. It indicates that the expressions on either side of the sign are equal in value.
- Function of the Equality Sign: It asserts a balance or equivalence between the two sides of the equation. This is the core principle that defines what is an equation.
- Solving Equations: To solve an equation, we manipulate the expressions on either side of the equality sign to isolate the variable, thereby finding its value. For example, in 2x + 3 = 7, the goal is to find the value of x that makes the equation true.
- Properties of Equality: Several properties, such as the reflexive property (a = a), symmetric property (if a = b, then b = a), and transitive property (if a = b and b = c, then a = c), underpin the concept of equations.
By understanding these components, we can better grasp what is an equation and how to approach solving it. Each part plays a crucial role in forming the mathematical statement and guiding us toward the solution. Recognizing and manipulating these elements accurately is key to mastering equations and their various applications in mathematics and real-world problems.
Types of Equations
Understanding what is an equation also involves knowing the different types. Here are some common types of equations:
- Linear Equations
A linear equation is an equation of the first degree, meaning it has no exponents greater than one. It can be written in the form ax + b = c, where a, b, and c are constants. An example is 2x + 3 = 7.
- Quadratic Equations
A quadratic equation involves terms up to the second degree. It takes the form ax^2 + bx + c = 0. An example is x^2 – 4x + 4 = 0.
- Polynomial Equations
Polynomial equations can have terms of varying degrees. For example: x^3 – 6x^2 + 11x – 6 = 0
- Rational Equations
Rational equations involve fractions with polynomials in the numerator and denominator. They look like (a(x)/b(x)) – c. An example is 2/(x+1) – 3.
- Exponential and Logarithmic Equations
Exponential equations have variables in the exponent, like a^x = b. Logarithmic equations involve logarithms, such as log(x) = b.
- Differential Equations
Differential equations involve derivatives of a function. They are essential in fields like physics and engineering.
How to Solve Equations
Now that we understand what is an equation and its types, let’s explore how to solve them.
Basic Techniques
- Addition and Subtraction
To isolate the variable, add or subtract the same value from both sides. For example, to solve x + 3 = 7, subtract 3 from both sides to get x = 4.
- Multiplication and Division
Multiply or divide both sides by the same value to solve for the variable. For example, in 2x = 8, divide both sides by 2 to get x = 4.
- Combining Like Terms
Simplify both sides by combining like terms. In 3x + 2x = 10, combine the x terms to get 5x = 10, then divide by 5 to get x = 2.
Advanced Techniques
- Factoring
For quadratic equations, factoring can simplify the solution. For x^2 – 5x + 6 = 0, factor to (x – 2)(x – 3) = 0, giving solutions x = 2 and x = 3.
- Using the Quadratic Formula
There is also a quadratic formula that can also be used to solve the equation. We simply have to put the formula and we will get the answer.
- Substitution and Elimination
For systems of equations, substitution and elimination are useful. Substitute one equation into another to solve, or eliminate a variable by adding or subtracting equations.
Equation vs. Expression
Understanding what is an equation involves distinguishing it from an expression. A common misconception is treating expressions as equations. Remember, an equation must have an equality sign indicating a relationship between two expressions.
Definitions
- Equation: A statement that two expressions are equal (e.g., 2x + 3 = 7).
- Expression: A combination of variables, constants, and operators without an equality sign (e.g., 2x + 3.
Key Differences
- Equality Sign: Equations have one; expressions do not.
- Purpose: Equations are solved to find the value of variables. Expressions are simplified or evaluated.
Examples
- Equation: 3x + 5 = 11
- Expression: 3x + 5
Common Mistakes and How to Avoid Them
When learning what is an equation, it’s crucial to avoid common mistakes.
- Misunderstanding Variables
Variables represent unknown values and can change. Misunderstanding this can lead to errors. Clearly define variables and consistently use them.
- Incorrect Operations
Follow the order of operations (PEMDAS: Parentheses, Exponents, Multiplication and Division, Addition and Subtraction, or BODMAS rule) to avoid mistakes. Incorrect operations can lead to incorrect solutions.
- Errors in Simplification
Simplify equations correctly by combining like terms and performing operations accurately. Double-check your work to ensure it’s simplified properly.
Conclusion
In summary, understanding what is an equation is essential for mastering mathematics. Equations are fundamental tools that balance two expressions, containing variables, constants, and operators. By learning about the different types of equations and how to solve them, you can unlock a deeper comprehension of math. Remember to practice regularly, avoid common mistakes, and use the techniques outlined in this article to enhance your skills. Share your experiences, ask questions, and let equations guide you to math success.
Frequently Asked Questions (FAQs)
What is an equation?
An equation is a mathematical statement that asserts the equality of two expressions, containing variables, constants, operators, and an equality sign.
How do you differentiate between types of equations?
Different types of equations include linear, quadratic, polynomial, rational, exponential, logarithmic, and differential equations, each defined by their specific forms and degrees.
How do you solve systems of equations?
Systems of equations can be solved using substitution, elimination, or graphical methods to find the values of variables that satisfy all equations simultaneously.
What is the difference between an equation and an expression?
An equation asserts the equality of two expressions and includes an equality sign, while an expression is a combination of variables, constants, and operators without an equality sign.