What is an Exponent and Exponent Rules? Demystifying Tiny Numbers with Big Impacts (2024)

Forget secret handshakes and hidden lairs, the true power of geniuses lies within exponent rules. These aren’t dusty old math codes, but the key to unlocking incredible calculations and understanding the universe

Exponents are like the superheroes of mathematics, quietly working behind the scenes to elevate numbers to new heights. In the realm of mathematical operations, exponents play a crucial role in simplifying complex calculations and expressing tiny numbers with monumental impacts.

This article will serve as your ultimate guide to understanding what an exponent is, unraveling the mysteries behind these powerful mathematical tools, and exploring the rules that govern their behavior. Whether you’re a math enthusiast or someone looking to demystify the world of exponents, this article is for you.

What is an Exponent?

Defining Exponents

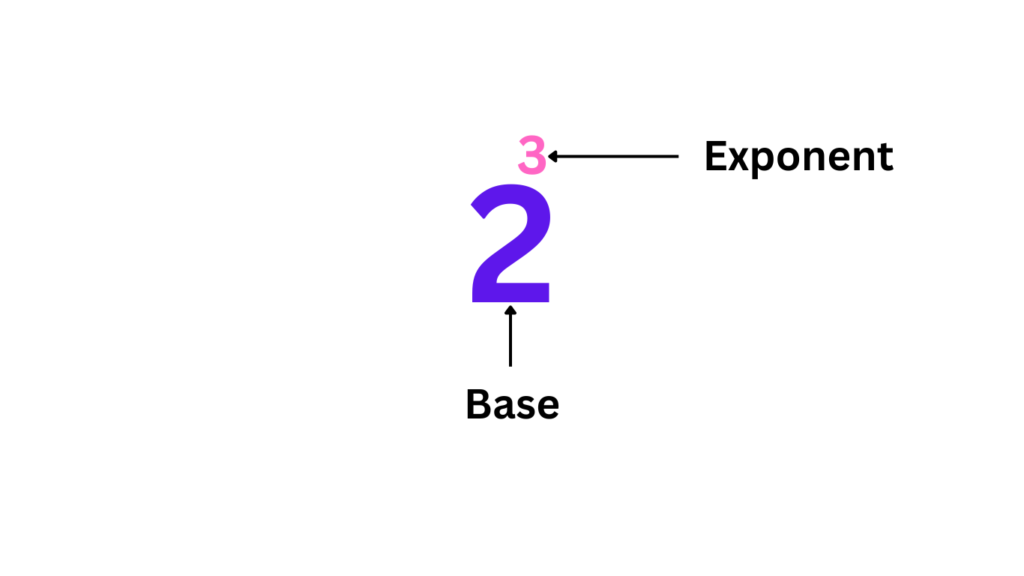
Exponents: An exponent represents the number of times a base number is multiplied by itself. It is denoted by a superscript number placed to the right and above the base number. For example, in the expression 2^3, the base number is 2, and the exponent is 3, indicating that 2 is multiplied by itself 3 times.

Understanding Exponential Notation

Exponential Notation: Exponential notation is a concise way of expressing repeated multiplication. It allows us to represent large or small numbers efficiently by using exponents. For instance, 10^6 represents 10 multiplied by itself 6 times, resulting in 1,000,000.

Exponent Rules

Basic Exponent Rules

• Product Rule: When multiplying two numbers with the same base, add the exponents. For example, a^2 * a^3 = a^(2+3) = a^5.
• Quotient Rule: When dividing two numbers with the same base, subtract the exponents. For instance, b^4 / b^2 = b^(4-2) = b^2.

Power Rule

• Power Rule: When raising an exponent to another exponent, multiply the exponents. For example, (c^2)^3 = c^(2*3) = c^6.

Zero and Negative Exponents

• Zero Exponent: Any number raised to the power of 0 equals 1. For example, x^0 = 1.
• Negative Exponent: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For instance, d^-2 = 1 / d^2.

Importance of Exponents

Exponents are not just mathematical tools; they have real-world applications that impact various fields:

Scientific Notation

Exponents are used in scientific notation to express very large or very small numbers in a compact form. This notation is essential in fields like astronomy, physics, and chemistry.

Compound Interest

In finance, exponents play a crucial role in calculating compound interest, where the interest is added to the principal amount, resulting in exponential growth over time.

Population Growth

Exponential functions model population growth, predicting the increase or decrease in population over time-based on factors like birth rate, death rate, and migration.

Role of Exponents in Mathematics

Exponents are fundamental in various mathematical concepts and operations:

• Algebra: Exponents are used to simplify algebraic expressions, solve equations, and manipulate variables.
• Calculus: Exponential functions and their derivatives play a significant role in calculus, especially in modeling growth and decay.
• Number Theory: Exponents are essential in number theory, exploring properties of prime numbers, factorization, and divisibility.

Application of Exponents in Daily Life Scenarios

Exponents are not confined to textbooks; they have practical applications in everyday life:

• Technology: Exponents are used in computer science to represent data sizes, memory capacities, and processing speeds.
• Engineering: Exponents are crucial in engineering calculations, such as determining power requirements, signal strength, and structural stability.
• Health Sciences: Exponents are utilized in medical research to analyze the exponential growth of diseases, drug dosages, and population demographics.

Significance of Exponents in Problem-Solving

Understanding exponents is key to solving complex mathematical problems efficiently:

• Scientific Research: Exponents are used to model natural phenomena, analyze data trends, and make predictions in scientific research.
• Financial Planning: Exponents help in calculating compound interest, investment growth, and loan amortization, aiding in financial decision-making.

Recognizing Exponents

Strategies for Identifying Exponents

Here are some tips to quickly recognize exponents in mathematical expressions:

• Look for Superscript Numbers: Exponents are often denoted by superscript numbers placed above and to the right of the base number.
• Identify Patterns: Exponents typically involve repeated multiplication or division, indicating the number of times a base is used.

Practical Examples Demonstrating the Application of Exponent Rules in Problem-Solving

Let’s explore how exponent rules can be applied to solve real-world problems:

Example 1: Calculate the value of 2^3 * 2^4 using the product rule. Solution: 2^3 * 2^4 = 2^(3+4) = 2^7 = 128.

Example 2: Simplify the expression (5^2)^3 using the power rule. Solution: (5^2)^3 = 5^(2*3) = 5^6 = 15625.

Practice Exercises to Reinforce Understanding of Exponent Rules

Test your knowledge of exponents with the following practice exercises:

• 2^4 = ? (Answer: 16)
• 5^0 = ? (Answer: 1)
• (3^2)^3 = ? (Answer: 729)
• 6^(-1) = ? (Answer: 1/6)

Conclusion

Exponents may seem like tiny numbers, but their impact is enormous in the world of mathematics and beyond. By understanding what exponents are and mastering the rules that govern them, you unlock a powerful tool that can simplify calculations, express large numbers efficiently, and solve complex problems with ease.

Recap of Key Points Covered in the Article:

• We defined exponents as the number of times a base is multiplied by itself and explored exponential notation for efficient representation of numbers.
• We discussed basic exponent rules, including the product rule, quotient rule, power rule, zero exponent rule, and negative exponent rule.
• We highlighted the importance of exponents in scientific notation, compound interest, population growth, and various fields of mathematics.
• We examined the role of exponents in algebra, calculus, and number theory, and their practical applications in technology, engineering, and health sciences.
• We provided strategies for recognizing exponents and practicing exercises to reinforce understanding of exponent rules.

Embrace the power of exponents in your mathematical journey, and watch as these tiny numbers make a big impact in your problem-solving skills and mathematical prowess.

Ways to Keep Exploring:

• Challenge yourself with advanced exponent problems and explore applications of exponents in different fields.
• Investigate real-world scenarios where exponential growth or decay occurs, and analyze the impact of exponents on the outcomes.
• Create your own exponent rules and test them with numerical examples to deepen your understanding of exponent operations.

Frequently Asked Questions (FAQs)

What are some common mistakes to avoid when working with exponents?

Common mistakes include forgetting the zero exponent rule, misapplying the power rule, and confusing positive and negative exponents. It’s essential to review exponent rules regularly to avoid errors.

How can exponents be used to simplify complex calculations?

Exponents allow for efficient representation of repeated multiplication, making it easier to handle large numbers, perform calculations quickly, and express relationships between quantities in a concise manner.

What are some real-world applications of exponential functions?

Exponential functions are used in finance to model compound interest, in biology to study population growth, in physics to describe radioactive decay, and in technology to analyze data trends and signal processing.