Have you ever heard of place value and got utterly confused or maybe you’ve helped your child with a math assignment, only to realize you’re a little fuzzy on the whole “ones, tens, hundreds” thing yourself?
Fear not, fellow number warriors. This article is your one-stop shop for understanding this mathematical concept, the secret code that unlocks the true meaning of numbers. Whether you’re a student seeking a clearer picture, a parent looking to brush up on the basics, or simply someone curious about the world of numbers, this guide is for you. We’ll delve into the exciting realm of place value, exploring its core concepts, applications in daily life, and fun tips to master it. So, grab your thinking cap and get ready to embark on a mathematical adventure!
Understanding the Building Blocks: Digits and Their Values
Before we dive into the magical world of place value, let’s establish our foundation. Numbers are made up of basic building blocks called digits. These little superstars, from 0 to 9, are the characters we use to write any number imaginable. Each digit has its own intrinsic value, but here’s the twist – the value of a digit can change depending on its place within a number. This is where the magic of place value truly comes alive.
Place Value
Imagine a grand palace with numerous rooms. Each room has a specific purpose and importance. Similarly, in the kingdom of numbers, each digit occupies a specific place, and its value is determined by that place. The further a digit is to the right of the decimal point (we’ll get to that fancy dot later!), the less its value becomes. Conversely, the further a digit is to the left of the decimal, the greater its value.
For instance, consider the number 321. The digit “3” is in the hundreds place, making it the most valuable digit in this number (3 x 100 = 300). The digit “2” resides in the tens place, giving it a value of 20 (2 x 10). Finally, the digit “1” sits in the ones place, holding the least value (1 x 1). By understanding where each digit lives within the number, we can grasp its true worth.
A Visual Tour: Exploring Using Number Line
Let’s take a visual stroll through the wondrous land of place value. Here’s a handy number line to help us navigate:
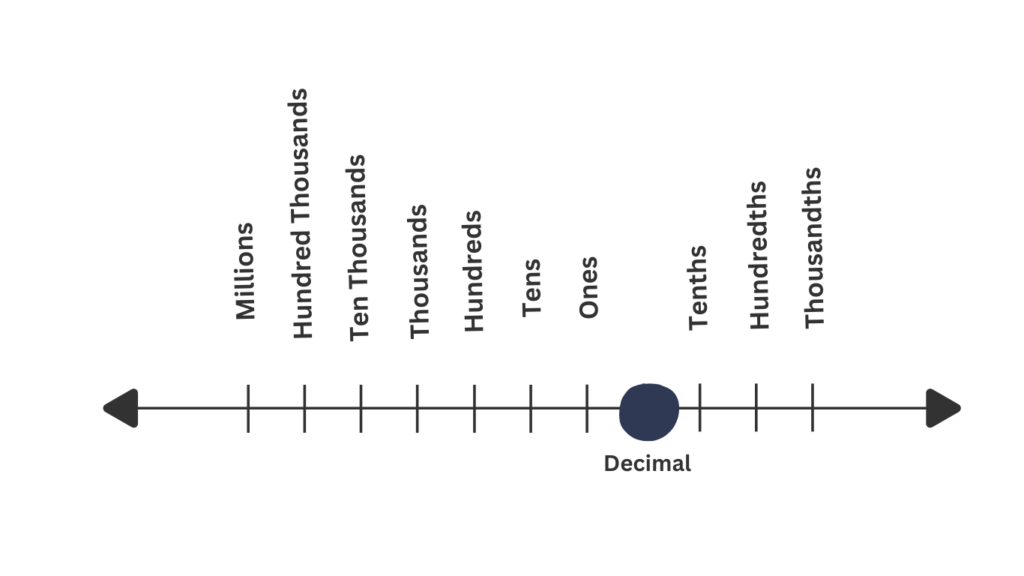
As you can see, the number line stretches infinitely in both directions, representing all the whole numbers we can imagine. Each section on the line is labeled with a place value term: ones, tens, hundreds, and so on. Notice how the value of each place increases by a factor of 10 as we move to the left.
Now, let’s see how place value affects the value of a digit within a number. Take the number 453. The digit “4” occupies the hundreds place (4 x 100 = 400), while the digit “5” is in the tens place (5 x 10 = 50). Finally, the digit “3” resides in the ones place (3 x 1 = 3). By understanding their place values, we can see that 453 represents four hundred fifty-three, not just a random sequence of numbers.
Introducing Decimals: A World Beyond the Whole
But wait, there’s more. The realm of place value extends beyond whole numbers. Enter the fascinating world of decimals. These tiny dots act as a dividing line, separating the whole numbers from their fractional counterparts. To the right of the decimal point, we encounter a whole new set of place values: tenths, hundredths, thousandths, and so on.
For example, consider the number 3.14. The digit “3” remains in the ones place, holding the value of 3. However, the digit “1” now occupies the tenths place (1 x 0.1 = 0.1), and the digit “4” resides in the hundredths place (4 x 0.01 = 0.04). When added together (3 + 0.1 + 0.04), we get the complete value of 3.14. Remember, decimals represent parts of a whole, and their place values reflect those fractional amounts.
A Peek at Negative Numbers
While not strictly related to place value itself, negative numbers can sometimes cause confusion. These numbers, denoted by a minus sign (-), represent values less than zero. The place value concept still applies to negative numbers, but their interpretation might differ slightly depending on the context.
For example, consider the temperature -5 degrees Celsius. Here, the “-5” occupies the ones place, indicating a value of 5 degrees below zero. The place values (tens, hundreds, etc.) would still follow the same principles as with positive numbers.
Place Value in Action: Making Numbers Work for You
Now that we’ve explored the core concepts of place value, let’s see how this magical skill benefits us in the real world. Here are some everyday situations where understanding it comes in handy:
- Reading Price Tags: Imagine comparing the price of apples at $1.25 per pound and oranges at $2.99 per pound. Identifying the place values of the digits allows you to quickly determine which fruit is the better deal.
- Following Recipes: Baking a delicious cake often involves precise measurements. Understanding how it affects teaspoons and cups ensures you add the correct amount of ingredients for a perfect outcome.
- Comparing Measurements: Whether you’re measuring lumber for a DIY project or tracking your child’s height growth, interpreting millimeters, centimeters, and meters requires a grasp of place value.
- Financial Literacy: From understanding interest rates on savings accounts to calculating percentages for discounts, this concept plays a crucial role in navigating the world of finance.
These are just a few examples, and the applications of place value extend far beyond everyday life. It forms the foundation for more advanced math concepts like multiplication and division, making it a vital skill for academic success in science, engineering, and other fields.
Mastering the Magic: Fun Tips and Tricks
Conquering place value might seem daunting at first, but fear not. Here are some engaging strategies to transform you into a pro:
- Place Value Games: Turn learning into a fun activity. Board games specifically designed for practicing place value can make the process interactive and enjoyable.
- Number Puzzles: Challenge yourself with puzzles that involve manipulating digits and their place values. These puzzles can sharpen your understanding in a stimulating way.
- The Power of Manipulatives: For visual learners, using physical objects like place value blocks can be incredibly helpful. These blocks represent different place values (ones, tens, hundreds) and allow you to see the relationships between them concretely.
- Sing a Song: Learning a catchy song about place values can be a surprisingly effective way to memorize the concepts. Rhymes and melodies can make the information stick in your mind.
- Practice Makes Perfect: The more you work with place value problems, the more comfortable you’ll become. Look for practice exercises online or in textbooks to solidify your understanding.
Common Challenges and Misconceptions
Even with a solid understanding of place value, people can sometimes encounter hurdles along the way. Let’s explore some common challenges and misconceptions along with tips to overcome them.
Identifying and Addressing Common Student Difficulties
- Confusing the value of a digit vs. the digit itself: Students might struggle to understand that the value of a digit depends on its position within a number. For example, the digit “5” in 51 represents 50, while the digit “5” in 500 represents 500. Using manipulatives like blocks with different colors for each place value can help visualize this distinction.
- Difficulties with decimals: The concept of tenths, hundredths, and thousandths can be tricky. Relating decimals to fractions (e.g., 0.5 is the same as 1/2) and using visual aids like grids can solidify understanding.
Tips for Overcoming Challenges in Teaching Place Value
- Make it concrete: Utilize manipulatives like blocks or counters to represent different place values. Students can physically move the blocks to see how the value of a digit changes with its position.
- Connect to real-world applications: Show students how it is used in everyday life, like reading price tags, measuring ingredients, or understanding weather reports (e.g., interpreting temperatures with decimals).
- Encourage active learning: Incorporate games, puzzles, and interactive activities to make learning place value engaging and fun.
Clarifying Misconceptions for a Stronger Foundation
- Thinking of all digits as equally important: Students might initially believe that each digit holds the same weight, regardless of its position. Highlighting the concept of increasing value as we move to the left in whole numbers and decreasing value to the right of the decimal point helps clear this misconception.
- Misunderstanding negative numbers: Negative numbers can introduce confusion. Emphasize that place value principles still apply, but the negative sign indicates a value less than zero.
Conclusion
By mastering place value, you unlock a whole new level of confidence in dealing with numbers. You’ll be able to tackle everyday tasks with ease, navigate complex calculations with a smile, and approach new mathematical concepts with a sense of empowerment. Remember, place value is the foundation upon which all other math skills are built. So, embrace the journey, have fun learning, and unlock the magic of numbers.
Frequently Asked Questions (FAQs)
What exactly is “place value,” and why is it important in math?
“Place value” refers to the value of a digit based on its position in a number. Understanding it is crucial because it helps us accurately interpret and manipulate numbers, ensuring precision in mathematical calculations.
How can I support my child in grasping the concept of place value?
To assist your child, engage in interactive activities, utilize visual aids, and incorporate educational games that make learning about place value an enjoyable experience.
What if I forget a specific place value term (like ten thousands)?
Don’t worry, that’s completely normal! There are many place value terms, and it is easy to get them mixed up sometimes. The key is to understand the basic concept: the value of a digit increases by a factor of 10 as you move to the left of the decimal point. So, if you forget a specific term, you can always figure it out by considering its position relative to the ones place and multiplying by the appropriate power of 10.